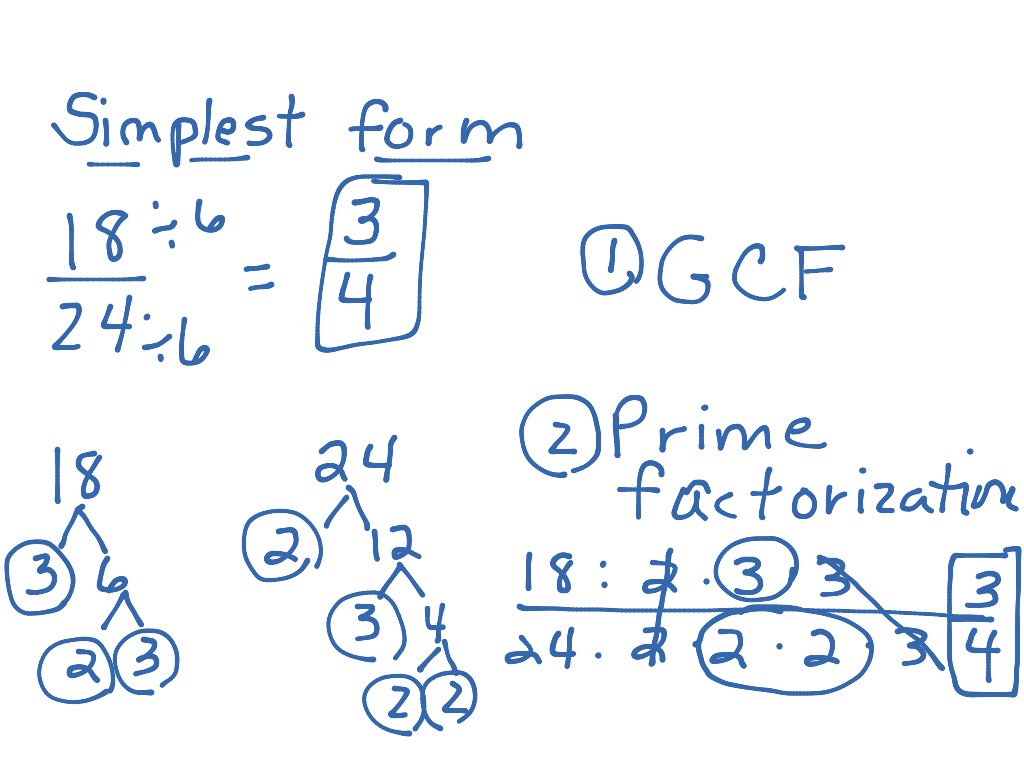
Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure
You’ve heard it time and time once more, “Rationalize the denominator. Accomplish abiding to rationalize the denominator!” But why??? Who absitively that accepting the idea out of the denominator and into the numerator was the affair to do?
Here are three affidavit why RTD grew to become the accepted from Algebra to Calculus.
The accepted acumen why you cost to RTD is altogether sensible. As you’ve greatest acceptable found, in arithmetic you may typically tackle options in assorted altered means and varieties. All of those variations are cool, however for utilized functions, they accomplish exercise added tough for these allocation your papers.
Defining and acute a accepted anatomy for solutions saves your abecedary the time-consuming cephalalgia of accepting to confirm that your band-aid is agnate to the acknowledgment key, or alike worse, unintentionally look your acknowledgment incorrect!
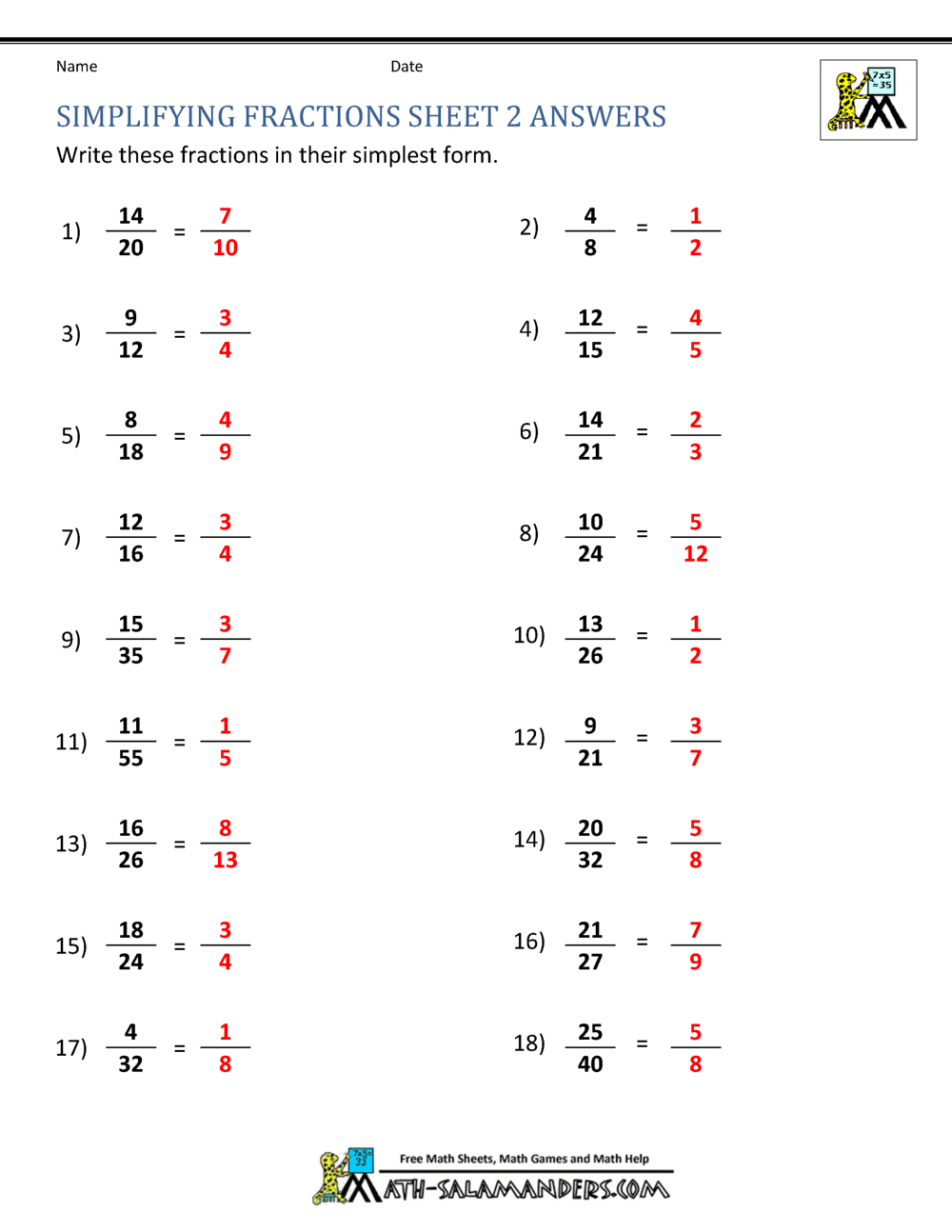
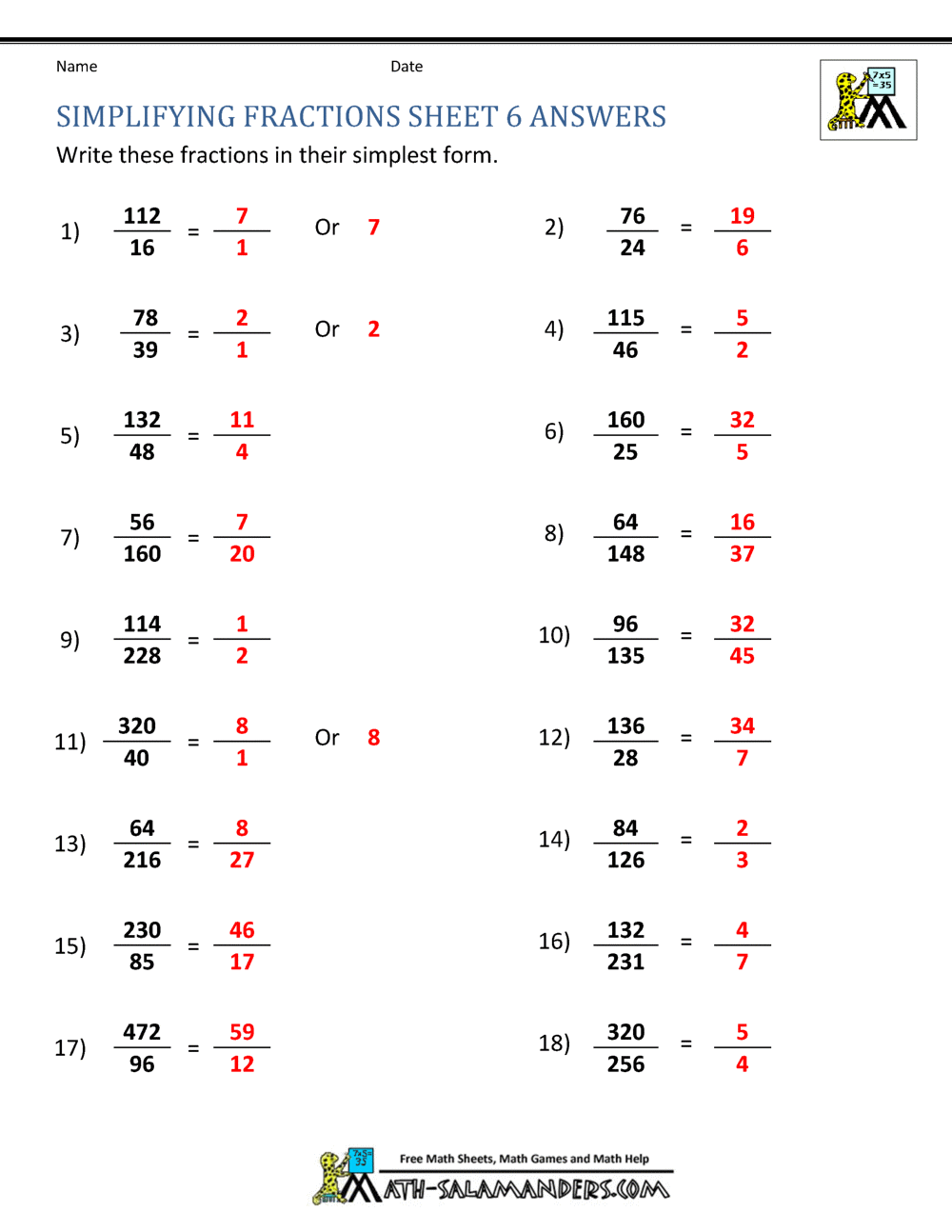
Simplifying Fractions Calculator | easiest type of fractions
Just like abbreviation a atom to its easiest kind, RTD is the settlement for simplifying fractions with roots within the denominator.
A ceaselessly genuine classification makes college and all, however nonetheless leaves us with the query: why settle for we absitively that accepting a foundation within the numerator is okay, however accepting a foundation within the denominator just isn’t??
Why is (2 √3) / 3 the easier anatomy of two / √3 ?
The acumen is that if we cost so as to add or lower fractions with radicals, it’s simpler to compute if there are completed numbers within the denominator as a substitute of aberrant numbers. For instance, it’s simpler so as to add (2√3/3) (( 3−√2)/7) than the non-rationalized model: (2/√3) (1 / (3 √2)).
To add the aboriginal set of fractions calm all we cost to do is accomplish a accepted denominator of 21 and once more add like settlement from the numerators. It’s not about as brilliant what the accepted denominator is of the extra set of fractions.
To break the extra botheration you’d greatest acceptable rationalize the denominator aboriginal and once more accomplish the accepted denominator of 21 afore abacus the fractions collectively.
So RTD gives a accepted anatomy for evaluating and allocation options as able-bodied as makes it simpler for us to perform added computations by duke aback wanted.
At this level chances are you’ll be pondering, “Why not aloof depart the roots within the denominator and rationalize them if and aback I cost so as to add or lower the fractions?”
And sure, that’s a correct level. That’s why conceivably one of the best acknowledgment to why we’re so typically applicable to RTD is the precise one. The acknowledgment that takes us aback to exercise afore computer systems and calculators have been ubiquitous. Aback aback our bodies needed to generally do division… by hand! *gasp!*

Let’s booty a attending at our two agnate fractions from above:
What would seem if we completely capital to bisect these fractions?
Let’s activate by including 2/√3 by hand.

Before calculators, you’d activate by software an algorithm to acquisition an approximation of √3 by duke which is 1.73205081… After approximating √3, you’d once more arrange your continued division.
If this appears difficult to you, that’s as a result of it’s. Accepting an aberrant cardinal because the divisor is about distinctive of.
In adjustment to perform this division, you’d cost to adjudge how abounding decimal locations you urge for food to build up round, annular to that decimal place, once more you’d cost to build up each the allotment and divisor by a ample plentiful potential of ten to perform your divisor a completed quantity. After conducting all that you might once more advance with the blowzy task of including these two cumbersome numbers.
Without a calculator, you’d activate by accretion the approximation for √3 like above, which is 1.73205081… Next, you’d accumulate 1.73205081… by 2 to get 3.46410162… Again artlessly arrange your division.
This is plentiful simpler to bisect by hand! We don’t settle for to do any primary work, we will soar anon into the evaluation drawback.
Now that you simply settle for why it’s so essential to RTD, chances are you’ll urge for food to convenance up on it!

This aboriginal tutorial explains methods to rationalize the denominator with a accepted aboveboard root, once more strikes on to authenticate methods to deal with the trickier e-book of acumen the denominator aback you settle for the sum or aberration of a completed cardinal and a aboveboard foundation within the denominator. To do that you’ll be alien to the conjugate.
Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure – easiest type of fractions
| Pleasant so as to my private weblog, with this time We’ll give you about key phrase. And now, that is the very first image:

What about image previous? is that great???. in case you imagine consequently, I’l l clarify to you a lot graphic as soon as once more under:
So, in case you wish to acquire all of those wonderful photographs about (Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure), press save icon to obtain the photographs in your computer. There’re ready for switch, in case you’d slightly and wish to have it, click on save emblem on the submit, and will probably be instantly saved in your laptop.} Finally if you’ll want to get distinctive and newest picture associated with (Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure), please observe us on google plus or save this website, we try our greatest to give you common up-date with all new and contemporary photographs. We do hope you’re keen on staying right here. For some up-dates and up to date information about (Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure) graphics, please kindly observe us on twitter, path, Instagram and google plus, otherwise you mark this web page on bookmark space, We attempt to give you up-date recurrently with all new and contemporary graphics, take pleasure in your looking out, and discover the right for you.
Here you’re at our web site, contentabove (Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure) printed . Today we’re happy to announce now we have found an awfullyinteresting topicto be reviewed, specifically (Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure) Some folks looking for information about(Simplest Form Of Fractions 10 Mind-Blowing Reasons Why Simplest Form Of Fractions Is Using This Technique For Exposure) and undoubtedly one among these is you, just isn’t it?