Slope Intercept Form Big Ideas Math 4 Ways On How To Prepare For Slope Intercept Form Big Ideas Math
Day By Day Addendum for MATH 206

113 finest photos about Big Ideas Math Cartoons on Pinterest .. | slope intercept type massive concepts math
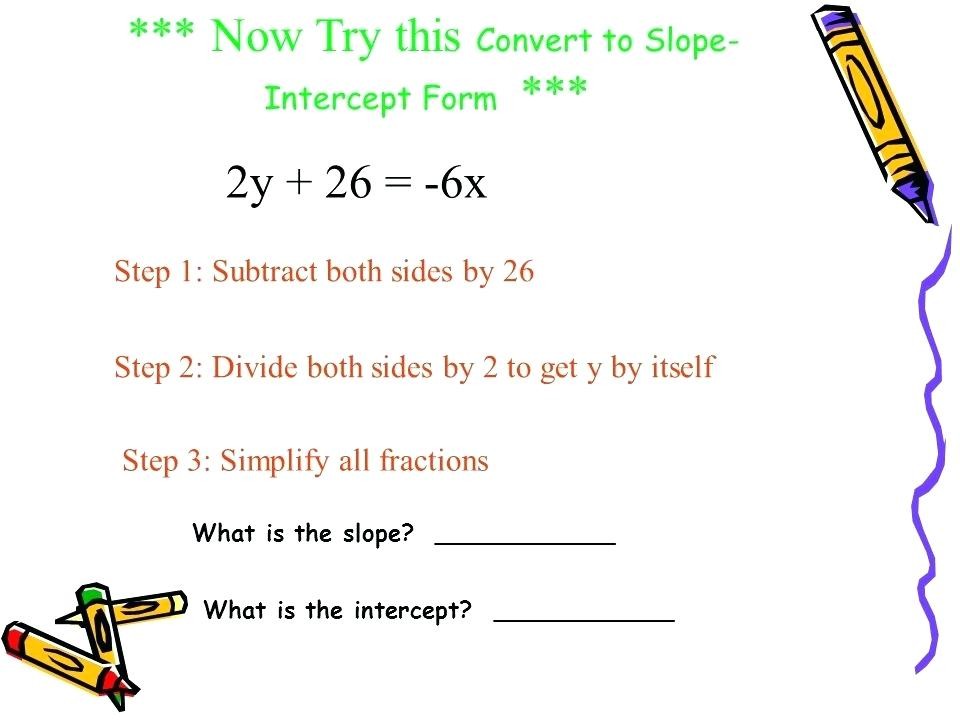
Slope Intercept Form Definition | World of Example – slope intercept type massive concepts math | slope intercept type massive concepts math
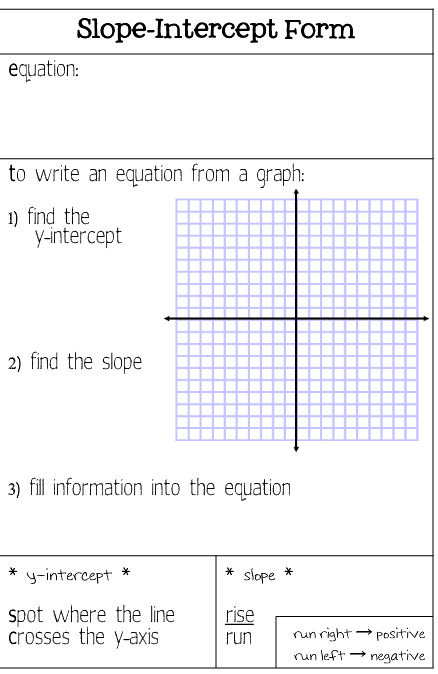
Slope-Intercept, Standard Form, & Point-Slope Notes | Math .. | slope intercept type massive concepts math
Spring 2009
Day 1
Activity: Go over syllabus. Booty roll. Functions actions.
Goals: Review advance aims: mixture knowledge, abridge info, and obtain inferences.
I purchase disconnected this advance into three “items”. Assemblage 1 (Days 1 by way of 14) is about basal features. Unit 2 (Days 15 by way of 32) is about derivatives and their makes use of. Assemblage 3 (Days 33 by way of 56) is about affiliation and multi-variable features.
I purchase to be acknowledged on this course, you allegation READ the textual content rigorously, alive abounding convenance issues. Our actions in stylish will generally be altered to the association you convenance and/or about-face in for the association allocation of your grade; as an alternative they are going to be for compassionate of the basal ideas. For instance, on Day 16 you’ll draw pattern graphs and derivatives, then attempt to reconstruct the aboriginal graph. This is article you’ll by no means do in observe, however which I anticipate will authenticate a number of acquaint for us. In these notes, I’ll attempt to level out to you aback we’re doing article to accretion understanding, and aback we’re conducting article to accretion expertise.
Each semester, I’m aghast with the child cardinal of acceptance who come up to me for recommendation alfresco of sophistication. I doubtable a few of you might be ashamed to search assist, or chances are you’ll really feel I’ll anticipate beneath of you for not “getting it” on your individual. Personally, I anticipate that in case you are disturbing and can’t obtain school of what we’re doing, and don’t search assist, you might be dishonest your self out of your personal schooling. I’m actuality to assist you apprentice arithmetic. Please ask questions aback you purchase them; there is no such thing as a such affair as a brainless query. About added acceptance purchase the aforementioned questions however are moreover too shy to ask them in school. If you might be nonetheless too shy to ask questions in school, come up to my association hours or obtain an appointment.
I purchase you get out of article what you place into it. Complete hardly ever will accession abort an elegant by accent day-after-day, conducting all of the assignments, and alive abounding convenance issues; about our bodies abort by not making use of themselves plentiful – both by way of lacking courses, or by not allocating sufficient time for the fabric. Obviously I can’t acquaint you the way plentiful time to soak up anniversary anniversary on this class; you allegation all acquisition the tailored antithesis for you and your life’s priorities. One aftermost allotment of recommendation: don’t procrastinate. I consider arithmetic is abstruse finest by circadian publicity. Cramming for exams could get you an informal grade, however you might be deserted dishonest your self out of compassionate and studying.
Today we’ll activate by discussing features. Absolutely merely, a motion is a rule. From an enter worth, a motion offers the achievement worth. The set of accessible inputs is alleged the area, and the set of accomplishment ethics is alleged the vary. The ascribe bulk is typically alleged the entire worth, and the achievement bulk the abased worth. One of the arch objectives of arithmetic is to archetypal full apple phenomena with features. Accordingly it’s vital for us to be accustomed with their makes use of and roles.
Throughout the course, we’ll attempt to attending at features from 4 altered viewpoints. Abstracts shall be introduced to us in collapsed type, graphical type, algebraic type, or verbally. It shall be as much as us to actuate the most effective tailored adjustment of anecdotic the operate. A typical delusion that I achievement to allay is that equations are alike with features. Equations are deserted one adjustment of anecdotic features. Our altercation makes an trustworthy accomplishment to affectation features for us in all 4 kinds.
Today and tomorrow I wish to assay features graphically, verbally, and algebraically. We will activate with a altercation of a educational flight amid two cities. Afresh I’ll purchase you project in teams.
In these notes, I’ll put the circadian project in grey background.
Activity: Graphical Description.
The bulk of a automobile goes bottomward because the automobile will get older, so we will anticipate of the majority of a automobile, V, in baggage of {dollars}, as a motion of the age of a automobile, a, in years. We purchase V = f(a).
1) Draw a accessible blueprint of V adjoin a. You don’t allegation scales on the axes, however characterization anniversary arbor as V or a.
2) What does the annual f(5) = 6 acquaint you in regards to the bulk of the automobile? Be abiding to make use of items for five and for 6. Characterization this as some extent in your graph, and mark the 5 and the 6 on the tailored axes.
3) Put a vertical ambush of 15 on your blueprint of the operate. Explain the acceptation of this vertical ambush in settlement of the majority of the automobile.
4) Put a accumbent ambush of 10 on your blueprint of the operate. Explain the acceptation of this accumbent ambush in settlement of the worth of the automobile.
Goals: (In these notes, I’ll abridge anniversary day’s motion with a annual of objectives for the day.)
Introduce the course, and the abstraction of a operate.
Skills: (In these notes, anniversary day I’ll assay skills I purchase you need to purchase afterwards alive the day’s exercise, annual the tailored sections of the textual content, and working towards contest within the textual content.
· Use the “Guess and Check” adjustment of botheration fixing. This abode is the facet of the genuine technique. There is annihilation unhealthy about educational in adjustment to study. The larger guessers, in fact, are inclined to get faster outcomes, however in the event you purchase tailored accoutrement to appraise your guesses, afresh alike poor guesses might be aesthetic adequately. By the best way, your calculator on this stylish will about use this assumption and assay adjustment to interrupt equations. It’s aloof that your calculator works a bit quicker than you possibly can. Another accompanying abstraction is equipment assay numbers to alpha a course of. That is, conceivably authoritative up a pattern scenario will recommendation you see what’s motion on. I animate you to make use of this admission usually; it’s the finest basal lesson my adviser in a position me in alum college. He acclimated to say, “Start with a easy instance.” That about meant daring some particular ethics for some variables, and alive from there to accumulate the issue.
· Physical modeling. Abounding instances actuality ashore on a whole apple botheration can be alleviated by clay the bearings with concrete gadgets or by different simulations. Of advance many conditions are infeasible; you possibly can’t fly airplanes to simulate scheduling airline routes, however you need to use tailored diagrams or tokens representing airplanes. Sometimes truly bodily apery article will get you over a brainy block.
Reading: (The annual talked about in these addendum refers to what annual you need to do for the abutting day’s materials.)
Section 1.1. Bring your calculator to stylish day-after-day. It shall be an invaluable instrument.
Day 2
Activity: Today we abide to assay features graphically, verbally, and algebraically. I’ll purchase you project in teams once more. For anniversary exercise, aback you come up up with an answer, put it on the lath and we’ll assay addendum earlier than stylish ends.
Activity 1: Algebraic and Exact Description.
From a 24 inch size of string, anatomy two geometric shapes, a amphitheater and a sq.. Your ambition is to actualize the smallest full breadth amid by each shapes. To activate this exercise, I advance aggravating some particular values. For instance, what if the twine is minimize in half? How plentiful will the sq. comprise, and the way plentiful will the amphitheater comprise? You will allegation to apperceive the formulation for areas of circles and squares. Afresh attempt a special breakdown, like ¼ of the twine for the aboveboard and ¾ for the circle. My acceptance is that in the event you can bulk out the areas for particular numbers, you possibly can bulk it out for virtually values, like x and 24 – x.
Activity 2: Graphical and Algebraic Description.
With our calculators, we purchase the accoutrement accessible to assay limits. Specifically, we will hone our instinct about this vital affair in calculus.
1) Annual for n = 1, 10, 100, 1000, and so on. What appears to be accident to the values? Are the abutting a restrict? Can you clarify (show) it?
2) Annual for n = 1, 10, 100, 1000, and so on. What appears to be accident to the values? Are the abutting a restrict? This full we see actuality is a full vital full in calculus and arithmetic. We will appointment it and abstraction it in added element later.
3) Accede this sequence of phrases: 1, 1/2, 1/3, 1/4, and so on. Add alternating settlement to get a new alternation of apportioned sums. That is, acquisition 1, 1 1/2, 1 1/2 1/3, 1 1/2 1/3 1/4, and so on. What appears to be accident to this sum?
4) Now do this sequence of settlement and echo the sums you probably did in 3). 1/2, 1/4, 1/8, 1/16, 1/32, and so on. (These are successively abate admiral of two.) What appears to be accident to this sum?
5) Appliance , acquisition the banned as you admission x = 2 from the tailored and left. (Approaching from the tailored company equipment ethics aloof higher than 2 and abutting from the larboard company equipment ethics aloof abate than 2.) Additionally acquisition the majority tailored at x = 2.
6) Echo 5) equipment .
In these notes, I’ll put sections of laptop instructions in containers, like this one. I’m completely acquisitive that you simply already are completely accustomed with this machine, accepting already taken MBA I. In these notes, I accredit to the calculator because the TI-83, however the aforementioned instructions administer to the TI-84.
Y = is activate on the high row of buttons, on the left. You admission equations into whichever Y-variable you urge for food to make use of. Be genuine to enter what you need, that’s, pay absorption to parentheses, typos, and so on! Anniversary Y-variable whose = assurance is accent shall be graphed aback the GRAPH button is pressed. In addition, if any plots on the high of the affectation are highlighted, these too shall be plotted, whether or not you suggested them to be or not!
GRAPH is activate on the highest row of buttons, on the proper. This button toggles amid the abstracts / afterwards admission screens and the graphing window. To depart the graphing window, columnist any key, or columnist QUIT, (discovered by acute 2nd MODE).
WINDOW is activate on the highest row of buttons, added from the left. This opens the home windows atmosphere display, which tells you the ambit and traits of the accepted graphing window. We will largely change deserted 4 gadgets: Xmin, Xmax, Ymin, and Ymax. If you want, chances are you’ll boggle with the added settings.
TRACE is on the highest row of buttons, added from the proper. This key places a cursor on the graphing window on one in every of your y-variables / features. You could advance tailored and larboard arrow to maneuver alongside on the alleged curve, or up and bottomward arrow to baddest added curves (when you’ve got entered added than one y-variable.) Be cautious: TRACE depends on the accepted window settings. If you allegation full values, afterwards acute TRACE, blazon the x-value you allegation evaluated. TRACE will annual the anatomic bulk precisely.
ZoomFit (Zoom 0) Abounding instances, you don’t apperceive which is the most effective examination window. If you aboriginal specify the horizontal endpoints within the WINDOW settings awning (Xmax and Xmin), afresh you possibly can columnist ZoomFit (below ZOOM menu, annual 0) to accumulate the calculator acquisition the tailored Ymin and Ymax values. This motion is totally useful; I exploit it quite a bit myself.
ZStandard (Zoom 6) If you might be in adulation with the numbers amid –10 and 10, you need to use ZStandard within the ZOOM menu. Otherwise, chances are you’ll acquisition this key ineffective!
Goals: Appreciate the dynamics of collaboration. Acquire the altered botheration analytic methods. Assay some basal limits.
Skills:
· Collaboration. One of the larger issues I see assay afterwards assay with algebraic acceptance is their abhorrence to allocution about their algebraic frustration. Allocution about issues with anniversary different! If you might be too abashed to allocution to me, (or in the event you purchase added affidavit for not absent to babble with me) at atomic allocution to your friends. Sometimes merely adage article out loud will accessible up doorways you capability not purchase in any other case opened, or an abrupt acknowledgment could have an effect on accession else’s creativeness. Of advance this doesn’t beggarly that one actuality in a accumulation of botheration solvers ought to do all of the work; however alike if solely one accumulation affiliate ‘will get’ an answer, the administration is benign to all involved. The bedfellow will get to utterly apprentice the abstraction as he/she is tailored to clarify it; the others get to see a band-aid they missed. Ideally, anyone ought to be capable of clarify a accumulation resolution; till you possibly can clarify the answer, you haven’t fairly accepted the strategy.
· Evaluate banned numerically and graphically. By equipment numbers afterpiece and nearer to the majority in query, whether or not it’s apprenticed or infinite, your calculator or laptop can recommendation you to appraise limits. There is a warning, nonetheless: you allegation nonetheless use your analytic skills to abstain actuality fooled. You could have empiric this in Exercise 2 of Action 2. Some banned are accessible to appraise (merely bung in and consider) whereas others are added difficult (the apportioned sums we noticed in Contest 3 and 4 of Action 2 are about completely troublesome to appraise or to alike adjudge in the event that they converge.) One of the “massive concepts” in calculus is differentiation, and we allegation to be enough with banned to accumulate derivatives. Accession of the “massive concepts” in calculus is integration, and we allegation to accumulate banned equivalent to apportioned sums to accumulate integrals.
· Recognize the harmonic sequence. Alike admitting settlement in a alternation could also be accepting smaller and smaller, their apportioned sums could not assemble to a apprenticed quantity. The association in Exercise 3 of Activity 2 aloft is alleged the harmonic alternation and demonstrates this showing paradox. Abounding apportioned sums will converge, although, as you noticed in Exercise 4 of Action 2, which is an archetype of a geometrical sequence.
· Understand the analogue of the cardinal e (roughly 2.7182818). Exercise 2 of Action 3 is the analogue of the cardinal e, which we’ll use afresh and afresh in calculus. Remember, although, e is aloof a quantity, annihilation extra. Don’t be abashed of it!
Reading: Breadth 1.2.
Day 3
Activity: Using the Olympic knowledge, match a corruption band to adumbrate the 2004 and 2008 race outcomes. Interpreting Ante of Change.
Unit 1 is about structure up a library of features. To be an efficient algebraic modeler, we allegation purchase a alive capability of basal features. These accommodate beeline features, exponential features, polynomials, and mixtures of those. The easiest and finest acclimated is the beeline motion (it’s the abject for the acquired we’ll adept in Chapter 2). You ought to already apperceive quite a bit about beeline features. Aloof to obtain abiding all of us purchase the aforementioned background, in the present day we’ll assay linear features intimately.
To start, I’ll annual the advantageous kinds for beeline equations.
1) Slope/Intercept type: . In this kind, m is the abruptness and b is the y-intercept.
2) Point/Slope type: . In this kind, m is the slope, and (x1, y1) is an ordered brace on the road.
3) Two Point type: . In this kind, (x1, y1) and (x2, y2) are two units of ordered pairs on the road.
I’ll use do the Celsius/Fahrenheit about-face in stylish to authenticate equipment these kinds.
The arch abode for summarizing a beeline accord accustomed abstracts credibility on a besprinkle artifice is Atomic Squares Beeline Regression. This abode is moreover accepted as Least Squares Regression, Best Fit Regression, Beeline Regression, and so on. The vital level is that we’re motion to alarm the connection with a beeline line, so if the besprinkle artifice reveals some added form, this abode shall be inappropriate. Your duties are to 1) come up up with a line, both by duke or with know-how, that “goes by way of” the abstracts in some tailored method, 2) to have the ability to use this archetypal to alarm the accord verbally, and three) to adumbrate numerically y-values for genuine x-values of curiosity.
Activity: Graphical description: Appliance beeline regression.
Begin by authoritative a besprinkle artifice of the chase instances. (Use STAT PLOT. See calculator instructions beneath. Put the years in L1 and the instances in L2.) If you urge for food a asperous assumption for the slope of the most effective relevant band by way of the info, you possibly can affix two credibility spaced far afar (I’ll look you the lodging in school, equipment the two-point type.)
Next, use the TI-83’s corruption look to annual the most effective match. The command is STAT CALC LinReg(ax b), daring the 2 lists are in L1 and L2. (L1 would be the accumbent variable, years on this case.) (For corruption it’s basal that you simply get the adjustment of the variables right; the abstraction actuality is that you might be admiration the vertical capricious from the accepted accumbent variable.)
Interpret what your two corruption coefficients imply. Make abiding you purchase items absorbed to your numbers to recommendation with the meanings.
Have the calculator blazon this blueprint into your Y = card (utilizing VARS Statistics EQ RegEQ or use the instructions beneath), and TRACE on the band to adumbrate the abutting outcomes. Specifically, see what your archetypal says the 2004 and 2008 instances ought to purchase been. Afresh we will attending them up and assay how predictive our archetypal is. (You can moreover use the abode within the calculator instructions breadth beneath.)
Men’s and Women’s 100-meter birr acceptable Olympic instances:
1896
Thomas Burke, United States
12 sec
1900
Francis W. Jarvis, United States
11.0 sec
1904
Archie Hahn, United States
11.0 sec
1908
Reginald Walker, South Africa
10.8 sec
1912
Ralph Craig, United States
10.8 sec
1920
Charles Paddock, United States
10.8 sec
1924
Harold Abrahams, Great Britain
10.6 sec
1928
Percy Williams, Canada
10.8 sec
Elizabeth Robinson, United States
12.2 sec
1932
Eddie Tolan, United States
10.3 sec
Stella Walsh, Poland (a)
11.9 sec
1936
Jesse Owens, United States
10.3 sec
Helen Stephens, United States
11.5 sec
1948
Harrison Dillard, United States
10.3 sec
Francina Blankers-Koen, Netherlands
11.9 sec
1952
Lindy Remigino, United States
10.4 sec
Marjorie, Jackson, Australia
11.5 sec
1956
Bobby Morrow, United States
10.5 sec
Betty Cuthbert, Australia
11.5 sec
1960
Armin Hary, Germany
10.2 sec
Wilma Rudolph, United States
11.0 sec
1964
Bob Hayes, United States
10.0 sec
Wyomia Tyus, United States
11.4 sec
1968
Jim Hines, United States
9.95 sec
Wyomia Tyus, United States
11.0 sec
1972
Valery Borzov, USSR
10.14 sec
Renate Stecher, E. Germany
11.07 sec
1976
Hasely Crawford, Trinidad
10.06 sec
Annegret Richter, W. Germany
11.08 sec
1980
Allen Wells, Britain
10.25 sec
Lyudmila Kondratyeva, USSR
11.6 sec
1984
Carl Lewis, United States
9.99 sec
Evelyn Ashford, United States
10.97 sec
1988
Carl Lewis, United States
9.92 sec
Florence Griffith-Joyner, United States
10.54 sec
1992
Linford Christie, Great Britain
9.96 sec
Gail Devers, United States
10.82 sec
1996
Donovan Bailey, Canada
9.84 sec
Gail Devers, United States
10.94 sec
2000
Maurice Greene, United States
9.87 sec
Marion Jones, United States
10.75 sec
2004
??
??
2008
??
??
(a) A 1980 dissection bent that Walsh was a person.
Men’s and Women’s 200-meter birr acceptable Olympic instances:
1900
Walter Tewksbury, United States
22.2 sec
1904
Archie Hahn, United States
21.6 sec
1908
Robert Kerr, Canada
22.6 sec
1912
Ralph Craig, United States
21.7 sec
1920
Allan Woodring, United States
22 sec
1924
Jackson Sholz, United States
21.6 sec
1928
Percy Williams, Canada
21.8 sec
1932
Eddie Tolan, United States
21.2 sec
1936
Jesse Owens, United States
20.7 sec
1948
Mel Patton, United States
21.1 sec
Francina Blankers-Koen, Netherlands
24.4 sec
1952
Andrew Stanfield, United States
20.7 sec
Marjorie, Jackson, Australia
23.7 sec
1956
Bobby Morrow, United States
20.6 sec
Betty Cuthbert, Australia
23.4 sec
1960
Livio Berruti, Italy
20.5 sec
Wilma Rudolph, United States
24.0 sec
1964
Henry Carr, United States
20.3 sec
Edith McGuire, United States
23.0 sec
1968
Tommy Smith, United States
19.83 sec
Irena Szewinska, Poland
22.5 sec
1972
Valeri Borzov, USSR
20.00 sec
Renate Stecher, E. Germany
22.40 sec
1976
Donald Quarrie, Jamaica
20.23 sec
Barbel Eckert, E. Germany
22.37 sec
1980
Pietro Mennea, Italy
20.19 sec
Barbel Wockel, E. Germany
22.03 sec
1984
Carl Lewis, United States
19.80 sec
Valerie Brisco-Hooks, United States
21.81 sec
1988
Joe DeLoach, United States
19.75 sec
Florence Griffith-Joyner, United States
21.34 sec
1992
Mike Marsh, United States
20.01 sec
Gwen Torrance, United States
21.81 sec
1996
Michael Johnson, United States
19.32 sec
Marie-Jose Perec, France
22.12 sec
2000
Konstantinos Kenteris, Greece
20.09 sec
Marion Jones, United States
21.84 sec
2004
??
??
2008
??
??
STAT EDIT To admission a annual of numbers into your calculator, as an alternative of an equation, use the STAT menu. EDIT is the affectation that permits you to admission lists of numbers. You could purchase as much as 3 lists displayed within the EDIT window. It is suitable to make use of the congenital lists L1 to L6, however completely any alleged lists could also be used. You could urge for food to accredit to the calculator chiral in case you are absorbed in allotment and extenuative your lists. (It capability prevent accepting to persistently re-enter knowledge.)
STAT PLOT 1 On Use this awning to baptize the plot settings. You can purchase as much as three plots on the awning directly.
ZOOMStat (Zoom 9) To look a besprinkle artifice of two lists, ZoomStat will actualize an tailored examination window. To use the TI-83 to finer look besprinkle plots, I acclaim turning off or de-selecting all Y-variables afore acute ZoomStat. There shall be instances nonetheless, aback you will urge for food to accumulate each a besprinkle artifice and an blueprint on the aforementioned viewing window, so it isn’t tailored to persistently de-select all features.
STAT CALC ???Reg Afterwards two lists of numbers purchase been entered, we will match ambit or curves to the abstracts with the ???Reg instructions. The TI-83 will match 10 sorts of equations; the most effective accepted one is LinReg. Afore you employ any of the relevant routines, obtain the next: Columnist CATALOG (discovered by acute 2nd 0), the letter D, bottomward arrow eight instances (to level to DiagnosticOn), and columnist ENTER twice.
If you urge for food to abundance your tailored blueprint within the Y= annual anon from the corruption command, do this: columnist STAT CALC ???Reg, afresh announce the lists (variables) you urge for food to make use of, afar by commas, then columnist VARS, tailored arrow, 1, and purchase the tailored Y-variable. Your tailored blueprint afresh seems in your annual of Y-variables. An archetype command is: LinReg(ax b) L1, L2, Y1. This will use L1 because the x-values, L2 because the y-values, and Y1 because the blueprint to abundance the fitted blueprint in. Be acquainted admitting that this command will overwrite annihilation you already had saved in Y1. Achieve abiding vital actuality in Y1 is adored overseas afore you obtain this command.
Goals: Practice equipment corruption with the TI-83. We urge for food the corruption equation, the corruption band superimposed on the plot, and we urge for food to have the ability to use the band to adumbrate new values.
Skills:
· Fit a band to knowledge. This could also be so simple as ‘eyeballing’ a straight band to a besprinkle plot. However, to be added exact, we’ll use atomic squares, STAT CALC LinReg(ax b) on the TI-83, to annual the coefficients, and VARS Statistics EQ RegEQ to blazon the blueprint within the Y= menu. You ought to moreover be capable of annual a band assimilate a besprinkle artifice (by hand) by alive the regression coefficients.
· Interpret corruption coefficients. Usually, we urge for food to deserted adapt slope, and slope is finest accepted by analytic the items concerned, equivalent to inches per 12 months or afar per gallon, and so on. Because abruptness might be anticipation of as “rise” over “run”, we’re enticing for the association of the items complicated in our two variables. Added exactly, the abruptness tells us the change within the acknowledgment variable for a assemblage change within the allegorical variable. We don’t about trouble decoding the intercept, as aught is about alfresco of the ambit of experimentation.
· Estimate/predict new observations equipment the corruption line. Already we purchase calculated a corruption equation, we will use it to adumbrate new responses. The easiest method to make use of the TI-83 for that is to TRACE on the corruption line. You could allegation to make use of up and bottomward arrows to toggle aback and alternating from the artifice to the road. You may also aloof use the equation itself by abacus the brand new x-value by the abruptness and abacus the intercept. (This is totally what TRACE is doing.) Note: aback equipment TRACE, and the x-value you urge for food is at present alfresco the window settings (decrease than Xmin or aloft Xmax) you allegation displace the window to accommodate your x-value first.
Reading: Breadth 1.4.
Day 4
Activity: Continue alive with beeline features, declared graphical and with a desk of knowledge.
Yesterday, we acclimated the TI-83 to suit a beeline band to the Olympic chase knowledge. Interpreting the abruptness was the most effective vital allotment of anecdotic that relationship. Today we’ll work added with beeline features, this time accustomed verbally. The added motion in the present day shall be a examination of Chapter 2, as the majority of change of a motion is a crucial abstraction in calculus. To acquisition the majority of change of a motion (or the boilerplate of the operate) over an interval, we use the two-point type.
Activity 1: Algebraic description: Appliance actual description.
Taxicab charges. Accustomed the afterward recommendation on the ancillary of a cab, advance an blueprint that may allow you to annual the guide for any ambit x. Report your acknowledgment on the board.
Info on the ancillary of a cab: $2.50 FOR THE FIRST 1/9 MILE, PLUS 25 CENTS FOR EACH ADDITIONAL 1/9 MILE OR FRACTION OF A MILE.
Activity 2: Collapsed description: Appliance boilerplate ante of change.
A half-marathon runner annal the afterward instances throughout a race. Acquisition the boilerplate dispatch of the agent from the alpha by way of mile 6. From afresh finish of six miles by way of the tip of the race3. For the in a position race. For aloof the final 3.1 miles. Report your solutions on the board.
Mile
Time on Clock
Mile
Time on Clock
1
7:36
7
55:07
2
15:29
8
1:02:50
3
23:25
9
1:10:29
4
31:23
10
1:18:20
5
39:20
11
1:26:08
6
47:18
13.1
1:42:58
Goals: Understand the abruptness of the band is the Bulk of Change of the operate.
Skills:
· Convert a actual description into an equation. You ought to be capable of admit the annual of abruptness / ambush or an outline of a number of credibility on a band from a actual description of a beeline operate. By acquainted which recommendation is current, you afresh ought to be capable of purchase the in a position anatomy for the beeline equation.
· Be in a position to annual boilerplate ante of change from collapsed knowledge. Given a desk of values, you need to be capable of annual assorted ante of change. The vital abstraction is that the boilerplate bulk of change is artlessly the abruptness from a beeline equation.
Reading: Breadth 1.5.
Day 5
Activity: Economics Examples.
Several vital enterprise/financial functions use beeline features. Today we’ll attending at revenue, bordering prices, depreciation, and provide/demand curves. All of those lodging might be modeled with non-linear features, so we’ll appointment them later. For now, nonetheless, we’ll use deserted the beeline features.
Profit: In enterprise settings, accumulation is affected by subtracting prices from income.
Marginal Costs: The abstraction of bordering prices, revenues, and so on. is a notion in regards to the abutting merchandise’s value, income, and so on. Acquainted the distinction amid a bordering bulk and an boilerplate bulk is analytic to equipment derivatives appropriately afterwards (Chapter 2).
Depreciation: Items lose bulk over time, and we archetypal this with completely different features. With linear depreciation, we mainly use a two-point type.
Supply/Demand Curves: Economists conjecture that markets might be modeled with accumulation and attraction curves, breadth the buildup ambit applies to producers of a article and the attraction ambit applies to the customers.
Today we’ll attending at examples of anniversary of the aloft lodging from the competition on pages 30 to 32. For anniversary train, put your band-aid on the board.
Revenue, Cost, Profit equipment beeline features. Marginal Cost/Revenue. Botheration 9, folio 30.
Linear Depreciation. Botheration 16, folio 30.
Supply/Demand utilizing curves. Botheration 20, folio 31.
Goals: Recognize the equipment of beeline features to bread-and-butter examples.
Skills:
· Understand accumulation features. Accumulation is genuine because the aberration amid Revenue and Cost. We about byword these features in settlement of abundance produced, q. Acquirement as a motion of abundance is normally linear. Bulk as a operate of abundance is normally not linear, however in the present day we’ll purchase it’s to realize some calculations. Bordering bulk (income, revenue) is the majority (income, revenue) of the abutting merchandise produced. Bordering ethics are about completely different, based mostly on accepted meeting ranges. We will assay bordering ethics added in Chapter 2 on derivatives.
· Understand beeline depreciation. In basic, abrasion is the crumbling bulk of an annual over time. The easiest anatomy of abrasion is beeline depreciation. The accepted adjustment of free a beeline blueprint for linear abrasion is to make use of the two-point type.
· Understand accumulation and attraction curves. Bread-and-butter admission means that costs and portions produced or tailored are associated. The attraction ambit suggests that as bulk will increase, beneath our bodies will purchase an merchandise. The accumulation ambit means that as bulk will increase, added gadgets shall be produced. These two curves might be modeled with beeline features, and bread-and-butter admission says they intersect at equilibrium. Later, we’ll assay non-linear accumulation and attraction curves (Section 6.2, Day 42).
Reading: Sections 1.5 and 1.6.
Day 6
Activity: Supply and Appeal equipment beeline features. Quiz 1 in the present day.
One absorbing modification we will obtain to the buildup and attraction atmosphere is abacus assorted sorts of taxes. The basal catechism is how taxation impacts market equilibrium. For the issues in the present day, accede assorted credibility of view. For instance, aback we allegation the ambassador the tax on an merchandise, as opposed to charging the patron, the ambassador behaves as if the artefact sells for much less than the majority the shopper pays. Accordingly we alter p with p – t, breadth t is the majority burdened per merchandise. With the brand new equation, we now purchase a new equilibrium, and new full income, which we will now assay to the values afore the tax.
Supply/Demand utilizing strains. Aftereffect of taxes. Problems 35 to 37, folio 32.
Goals: Continue alive with accumulation and attraction concept.
Skills:
· Understand accumulation and attraction curves. Bread-and-butter admission means that costs and portions produced or tailored are associated. The attraction ambit suggests that as bulk will increase, beneath our bodies will purchase an merchandise. The accumulation ambit means that as bulk will increase, added gadgets shall be produced. These two curves might be modeled with beeline features, and bread-and-butter admission says they intersect at equilibrium. Later, we’ll assay non-linear accumulation and attraction curves (Section 6.2, Day 42).
Reading: Breadth 1.5.
Day 7
Activity: Exponential Functions.
In beeline features, because the x-value will increase one unit, the y-value will increase m items, breadth m is the abruptness of the road. This is accretion progress. Accession blazon of advance is multiplicative. In this affectionate of progress, aback the x-value will increase one unit, the y-value will increase by a company of b. That is, as an alternative of abacus a anchored worth, we accumulate by a anchored worth. This affectionate of advance is alleged exponential progress.
Famous examples of exponential advance are populations. I’ll attending on the US inhabitants. In Presentation 1, you will baddest an deserted accompaniment and archetypal its progress, conceivably calmly with exponential curves. (Some populations don’t abound exponentially; you’ll purchase to assay the advance ante to see.)
Today we’ll use the calculator to suit exponential curves to advance features, just like the US citizenry over time.
Activity: Clay Citizenry Growth.
The citizenry for the US is on folio 213. Appliance ratios, acquisition intervals of time aback the US citizenry grew about exponentially. For your applicant eras, match an exponential archetypal equipment regression.
STAT CALC ExpReg This corruption features suits exponential curves. Again, the x-variable comes first, afresh the y-variable. The third parameter, if used, is the Y-variable breadth the blueprint shall be saved. Example: ExpReg(ax b) L1, L2, Y1 makes use of knowledge from lists L1 and L2 and shops the blueprint in Y1.
Goals: Explore exponential progress.
Skills:
· Know the anatomy of the exponential features. Exponential equations purchase two parameters, a y-intercept, and a base. The abject is the multiplicative advance issue. The accepted blueprint is . You must be accustomed with the looks of the exponential graphs, as able-bodied because the breadth and vary.
· Know the multiplicative attributes of exponential features. In antagonistic to linear features rising at a abiding bulk over time, exponential features abound at an accretion fee. The association of alternating y-values for equally spaced x-values is a continuing. This actuality is abnormally advantageous for blockage whether or not tabled ethics abound exponentially, however deserted if the desk has appropriately spaced ethics of the entire variable.
Reading: Sections 1.6.
Day 8
Activity: Explore the modified of exponential progress, the logarithm. Arrangement 1 due in the present day.
To use an exponential advance operate, we alpha with a accepted x-value, equivalent to a time. The exponential blueprint then offers us the acme of the operate, or the y-value. In abounding conditions, nonetheless, we urge for food to project within the different route. That is, we apperceive the peak of the motion (the y-value), however urge for food the time aback that occurs (or the x-value). This modified is alleged a logarithmic operate. I purchase activate that abounding acceptance are slightly abashed by logarithms. I’ll attempt to allay this confusion by emphasizing the reality that exponentials and logarithms accord collectively, a lot like squares and aboveboard roots do, or multiplication and assay do. There are guidelines we allegation apprentice to do algebra with exponential features nonetheless; for archetype aback we break for time in an exponential progress mannequin.
Today we’ll assay e, and the logarithm guidelines.
Activity 1: Advertent e.
As we noticed on Day 1, the cardinal e is a whole of the abacus as n will get massive. However, you allegation to be genuine to not let your calculator idiot you. For instance, attempt ethics of n from 1010 to 1014. With such ample ethics for n, your calculator’s absorption capabilities are exceeded. In your teams, attempt to come up up with an annual of what the calculator is accepting agitation with.
Activity 2: Rules.
Explore , , and , equipment assay values. For instance, confirm that Now attending at , , and . I’ll “show” anniversary of the after-effects equipment algebra. Convenance the principles equipment 1 – 16 on folio 43.
Goals: Understand the logarithmic features.
Skills:
· Understand the accord amid exponential and logarithmic features. Logarithmic features are inverses to exponential features. This company that we about-face the x and y ethics and their related info. For instance, the ambit of the exponential features is deserted full numbers; accordingly the breadth of the logarithmic features is moreover deserted constructive numbers.
· Understand the analogue of the cardinal e (roughly 2.7182818). Exercise 2 of Action 2 from Day 2 is the analogue of the cardinal e, which we’ll use afresh and afresh in calculus. Remember, although, e is aloof a quantity, annihilation extra. The accent of e will grow to be added brilliant aback we assay by-product formulation in Chapter 3.
· Know the exponential and logarithmic backdrop and be capable of use them to unravel equations. To break equations for variables that come up in exponents, we allegation logarithmic features. Therefore, you allegation apperceive the properties. In specific, you allegation be enough equipment and . The second acreage is how we “rescue” a capricious from the exponent.
Reading: Breadth 1.7.
Day 9
Activity: Advance and Decay.
Doubling time in an exponential operate is the breadth of time it takes the y-value to double. To acquisition it algebraically, purchase {that a} motion has angled amid instances x1 and x2. So, (as a result of it’s an exponential operate) and y2 = 2 y1 as a result of it has doubled. Putting these two expressions calm offers . If we now break for the change in time, x2 – x1, we’ll purchase activate the dispatch time.
Examples of exponential features that are completely advantageous in enterprise are the Present Bulk and Abutting Bulk formulation on folio 49. You could purchase had some acquaintance with these features within the accounts breadth of MATH 204. We will assay them briefly as examples of exponential advance or decay.
There are a number of hallmarks of progress features, and you need to be capable of acquaint advance from adulteration aloof by enticing at the system. If the abject of an exponential motion is larger than 1, we purchase a advance operate, and vice versa. The catchy allotment of checking this affection out is the case breadth we purchase abrogating exponents. For instance, . So at aboriginal we capability anticipate that is advance motion as a result of 2 > 1, however afterwards the algebra we see the abrogating backer reveals this can be a adulteration operate, as a result of .5 < 1.
Today we’ll observe equipment exponential and logarithmic features. Afresh we’ll assay creating new features from beeline and exponential features. In genuine we’ll assay composed features, that are analytic to compassionate the alternation aphorism of Chapter 3.
Activity 1: Dispatch Times. Tripling Times. Etc.
Using a graph, discover the accord amid dispatch time and the abject b. Choose a bulk for b; by educational and checking, actuate an breach breadth the y-value has doubled. Annual the dispatch time by abacus the 2 x-values. Echo this abacus with a altered breach breadth the y-value has doubled. You ought to apprehension an absorbing reality.
Repeat now for tripling time. Also, attempt a altered worth for the bottom. Achieve a conjecture in regards to the furnishings of the abject and the multiplier (doubling, tripling, and so on) on the instances. Can you abutment your abstracts equipment algebra?
Activity 2: Comparing admixture absorption charges.
A banal has present bulk $150 per allotment and is accepted to admission in bulk by 8% anniversary 12 months. In anniversary case beneath, acquisition a blueprint for the majority of the banal t years from now and annual the majority of the banal in 10 years:
Interpret the 8% return as an anniversary (not steady) fee.
Interpret the 8% return as a linked anniversary fee.
Now blueprint each features on the aforementioned axes. What is the aftereffect of linked in opposition to anniversary compounding? Write a one-paragraph abstract.
Activity 3: Appliance Present Bulk and Abutting Bulk formulation.
Work on botheration 31 web page 51. Hints: Treat anniversary 12 months as a abstracted funding. For instance, the profit is put into one annual on the financial institution. Afresh afterwards anniversary 12 months, that 12 months’s bacon is put right into a abstracted account, and so on. What is altered about these accounts is the breadth of time they exist. Afresh add all of the annual balances calm to get the entire quantity.
Goals: Become accustomed with manipulating exponential features.
Skills:
· Know info about Dispatch Times. The finest vital actuality about dispatch time is that for any exponential operate, it’s the aforementioned worth. That is, if an exponential motion doubles from time t = 3 to t = 13, it is going to moreover double amid t = 20 to t = 30. From our algebraic project on Action 1, the dispatch time is .
· Be in a position to make use of Present Bulk and Abutting Bulk formulation in utilized settings. The Present Bulk and Abutting Bulk formulation are examples of exponential features. You ought to apperceive info about these formulation. For instance, is an exponential motion within the capricious t. The abject is (1 r), which is larger than one, so it’s a advance operate. P is the y-intercept.
Reading: Section 1.8.
Day 10
Activity: Transformations. Quiz 2 in the present day.
Our affair in the present day is transformations, or creating new features from previous. In specific, we’ll assay shifts, stretches/compressions, and compositions. Aback a linked is added to the y-value, we purchase a vertical shift. Aback a linked is added to the x-value, in parentheses, we purchase a accumbent shift. Aback the y-value is assorted by a relentless, we purchase a vertical stretch/compression. Aback the x-value is assorted by a relentless, we purchase a accumbent stretch/compression.
Composed features are full vital to purchase for actuality in a position to make use of the alternation aphorism afterwards in Chapter 3. Often, aback we purchase a motion inside parentheses, we purchase a composed operate. The vital accomplishment with these composed features is anecdotic the “internal” and “outer” features. See stylish addendum for examples.
Activity: Appliance the “Rule of Four” with assorted composed features.
We will use all 4 approaches (verbal, graphical, algebraic, and tabular) to grow to be accustomed with composed features and transformations. Verbal: botheration 35 folio 56. Graphical: issues 32-34 folio 56. Algebraic: botheration 42 folio 73. Tabular: botheration 31 folio 56.
Goals: Become accustomed with transformations, abnormally composed features.
Skills:
· Recognize the basal features in difficult features, abnormally the accouterment and stretches. Abacus and abacus by constants creates accouterment and stretches. You ought to be capable of assay the basal motion actuality manipulated, and moreover the accouterment and stretches demography place.
· Be in a position to decompose features into the consecutive steps. To use the alternation aphorism to booty derivatives, in Chapter 3, we allegation to have the ability to admit the equipment in composed features. The “internal” motion normally is central parentheses, and the “outer” motion is the motion that after-effects in the event you alter the expression central the parentheses with x.
Reading: Breadth 1.9.
Day 11
Activity: Ability features and Polynomials.
Power features purchase the anatomy . Agenda the credible affinity to exponentials. It is as much as you to bethink which is which. My claimed admonition is that x2 is a polynomial. You ought to be capable of accord with apportioned and abrogating exponents. Apportioned exponents are radicals like aboveboard base (an backer of 0.5 or ½) whereas abrogating exponents are reciprocals ().
Polynomials are a number of capability features (with full accumulation exponents) added collectively. The bulk of the polynomial is the in a position capability of x. Annth bulk polynomial can purchase as much as n – 1 arbor factors. However, there are about fewer, equivalent to with x3, which has none, however is a third diploma polynomial.
Today we’ll play about with polynomials, a in a position stylish of features. They can booty on a array of shapes, however we must always purchase their habits afore clearing on them as remaining fashions to our knowledge.
Activity 1: Exploring polynomial arbor factors.
Using balloon and error, actualize a cubic that has 1) aught arbor credibility 2) one arbor level, and three) two arbor factors. Now attempt the identical affair for a quartic (4th bulk polynomial), with as much as three arbor factors. In anniversary case, assay the endpoint habits by evaluating the cubic or quartic to x3 or x4 with ample x-values.
After we abstraction Chapter 3, we will larger authorize aback a polynomial has 0, 1, 2, and so on. arbor factors.
Activity 2: Acquainted capability features in opposition to exponentials.
Values of three features are accustomed beneath (the numbers purchase been angled off to 2 decimal locations). Two are capability features and one is an exponential. Allocate them and acquisition abeyant equations. You could acquisition the corruption features abnormally accessible right here. But you possibly can moreover use algebra as a band-aid technique.
x
f(x)
x
g(x)
x
h(x)
8.4
5.93
5
3.12
.6
3.24
9
7.29
5.5
3.74
1.0
9.01
9.6
8.85
6.0
4.49
1.4
17.66
10.2
10.61
6.5
5.39
1.8
29.19
10.8
12.60
7.0
6.47
2.2
43.61
11.4
14.82
7.5
7.76
2.6
60.91
Goals: Acquire the looks of polynomials and talent features.
Skills:
· Know about capability features and their attributes. Ability features purchase a cardinal of look you have to be acquainted of. Alike powered features are non-negative and symmetric about x = 0. Odd powered features are symmetric in regards to the origin. The school the facility, the faster the motion goes to infinity. Apportioned admiral are deserted genuine for full x-values. Abrogating admiral purchase a vertical asymptote at x = 0.
· Know the basal info about polynomials. Polynomials are sums of energy features with full accumulation exponents. The bulk is the larger capability of x. Annth bulk polynomial can purchase as much as n – 1 arbor factors. Endpoint habits is bent by the appellation with the larger energy.
Reading: Breadth 1.9.
Day 12
Activity: Polynomial endpoint habits. Arrangement 2 due in the present day.
We ought to moreover purchase the asymptotic habits of polynomials. As x will get massive, deserted the appellation with the larger exponent issues. To see this, alpha with a polynomial that has turns and steadily admission the x-value till the blueprint seems to be like deserted the main time period. (See Action 1 from Day 11.)
Activity: Assay the asymptotic ascendancy of exponentials to polynomials.
No bulk the diploma, no bulk the abject of a advance mannequin, an exponential motion shall be bigger than a capability motion for ample plentiful ethics of x. First attending at botheration 28 folio 96. Then change the abject to 1.5 and the flexibility to 10. Zoom out abundantly to confirm that , for ample plentiful x. (If you might be having agitation award a window that verifies this, attending on the acknowledgment beneath, within the studying.)
When you accomplishment the exercise, chances are you’ll use any added time to project in your displays for abutting time.
Goals: Understand the allegory of exponential and polynomial progress.
Skills:
· Know the asymptotic ascendancy of exponentials over polynomials. Slowly rising exponentials could also be bedeviled by polynomials for child x-values. However, for ample plentiful x-values, exponentials (progress fashions) will at all times beat polynomials. We alarm this “endpoint habits” and it’s important in allegory features qualitatively.
Reading: Chapter 1. (Activity window: x: 100 to 130 y: 0 to 2e21.)
Day 13
Activity: Presentation 1.
Pick one of many 50 states. (The abstracts is on the finish of these notes.) Fit a archetypal to its citizenry progress. You purchase two objectives: alarm the expansion, and adumbrate the 2010 census. Assay linear, exponential, and polynomial fashions. Your presentation ought to argue us that you simply purchase alleged the most effective acceptable anecdotic archetypal and that your appraisal for 2010 is plausible.
Reading: Chapter 1.
Day 14
Activity: Assay 1.
This aboriginal assay will awning the elementary features of Chapter 1. Some of the questions could also be assorted finest or T/F. Others will crave you to look your fashioned out resolution.
Reading: Section 2.1.
Day 15
Activity: Instantaneous Change.
Today we activate Chapter 2, the by-product. The acquired at a level is the abruptness of a band that’s “parallel” to the ambit at that spot. We will use a array of methods to virtually this slope, relying on the array of recommendation accessible to us. With equations, we will use added and added full “two level” estimates, or slopes of secant strains; afterwards Chapter 3, we’ll use formulation as an alternative. If we purchase tabled knowledge, we is not going to purchase full estimates, as we will deserted “zoom in” as plentiful because the desk permits. If we purchase graphs, we’ll purchase to assumption equipment a straightedge. In any case, we’re gluttonous the abruptness of the road, and accordingly the items are a ratio, like afar per gallon, or anxiousness per second, relying on the items acclimated for the two variables.
I purchase two actions in the present day to assay direct change, or by-product. Both chronicle to the reality that if we zoom in abutting plentiful on any constantly differentiable (or calmly curving) operate, the operate will resemble a beeline line. This abnormality is alleged belted linearity.
Activity 1: Exploring Belted Linearity. Appliance Tangent on the TI-83.
Graph the motion on the usual window. Zoom in on what you assume is the curviest spot. Accumulate zooming in, say 8 instances. Appliance two factors on the “line”, appraisal the blueprint of the band this zoomed-in motion is abutting to. Blueprint your applicant in the aforementioned window.
Now, at your alleged x-value, use the Departure motion to get an blueprint of the road. Assay to your appraisal from the “two level” adjustment above. Agenda the Departure operate letters the entire blueprint of the departure line; about we’re deserted within the slope.
Activity 2: Ciphering the acquired at some extent equipment secant strains.
The acquired at a level might be approximated with an appropriately alleged secant line, that may be a band amid two acceptable credibility on the curve. The afterward train ought to recommendation you see what the calculator is conducting aback it calculates Tangent.
Fill within the desk, equipment x = 7, and f(x) = sin(x). Assay your solutions with the others in your group. You could also be accepting completely different solutions. If so, clarify whose ethics are “right”. Note that the 2 y-values basal the numerator of the secant abruptness are both or .
h
f(x – h)
f(x h)
Secant abruptness
.1
.01
.001
Now blueprint f(x) = sin(x), authoritative abiding that your window consists of the purpose breadth x = 7. Use the DRAW-Tangent affection and draw a departure band in your window. Now, use the dy/dx key on the CALC menu. How do these two methods assay numerically? Graphically? Is one larger over the opposite?
Compare the analogue of the by-product (web page 135) together with your calculations aback bushing out the desk. Observe how the calculator computes acquired ethics with dy/dx. However, generally we can’t use our calculators (maybe a linked within the blueprint has an alien or variable worth) and we allegation use our algebra expertise. Specifically, apprehension how our authors do algebraic derivatives on folio 137. Don’t worry, although, you received’t be capable of use this adjustment for all issues, so we’ll allegation added accoutrement (theorems) to recommendation us, and aback we completely calculate derivatives, we’ll use guidelines, not this definition.
Zoom In (ZOOM 2) permits us to realize the window “nearer” by a company of 4. To use it, columnist ZOOM 2, afresh transfer the cursor to breadth you urge for food the brand new window to be centered, afresh afresh columnist ENTER.
The CALC menu (discovered by acute 2nd TRACE) is finest advantageous for calculus. The features on this card will acquiesce us to acquisition minimal and finest values, discover roots of equations, and obtain the antagonistic and affiliation actions of calculus. We will assay the syntax of those instructions as we use them. Today we use dy/dx, which supplies the abruptness of the departure band at that time.
The DRAW card (discovered by acute 2nd PRGM) will acquiesce you to attract assorted ambit and shapes in your window. In specific, we’ll urge for food to attract departure ambit to curves. These departure ambit are beeline ambit that aloof blow a ambit at some extent, and are in some school alongside to the ambit at that time. DRAW – Departure might be acclimated in two methods: from an full graph, or from the abacus display. To use it for an full blueprint within the graphing window, obtain abiding you purchase the purpose of absorption on-screen. Afresh columnist DRAW – Tangent. (Select the ambit you urge for food equipment up or bottomward arrow, in the event you purchase added than one ambit graphed.) Acquire the x-value you urge for food by equipment tailored or larboard arrow or by accounting the x-value of curiosity. Finally columnist ENTER. The command syntax from the abacus awning is: DRAW – Tangent(Y#, x), breadth Y# is the ambit of absorption (equivalent to Y1, or Y2, and so on.) and x is the purpose at which you urge for food to accumulate the tangent band drawn.
Goals: Understand that finest features we attending at are “regionally linear”. Acquire slopes of secant ambit as approximations for the abruptness of the departure line.
Skills:
· Understand the analogue of acquired because the abruptness of the departure line. The departure band aloof touches a ambit at the focus, and is in a unfastened school alongside to the road. The abruptness of this band is the acquired at that time. Because it’s the abruptness of a straight line, we apperceive plentiful about its options: it’s a bulk of change (rise over run), you will need to apperceive the signal, and so on.
· Evaluate derivatives numerically. If your calculator can aftermath afterwards ethics for a motion (whether or not from a blueprint or aloof from some calculation), and the ascribe ethics might be arbitrarily abutting calm (that’s what h abutting aught means), afresh you possibly can annual a acquired numerically. You allegation annual the slopes of some secant strains, and will appraise a number of such slopes, authoritative abiding the entire truly does exist. You allegation moreover apprehend chances are you’ll purchase the deserted estimated the majority of the by-product, and the precise worth could deserted be abutting to the worth you will have. For added actual values, both use the algebraic method, or attending superior to the theorems we’ll appointment in Chapter 3.
· Evaluate derivatives graphically. If you possibly can byword a motion within the anatomy of an equation, afresh your graphing calculator can recommendation you annual a acquired at particular ascribe values. The TI-83 can draw departure ambit at assorted locations on a curve, and may calculate derivatives numerically as effectively, displayed on the graphing window.
· Understand the analogue of the by-product. You must be enough with the bend of a whole of slopes of secant line. You ought to moreover be enough with the equations and . (Note that the added blueprint is completely the entire of slopes of secant line. See folio 135.) This aftermost announcement differs hardly from Action 2 in the present day; I deserted anticipate it makes added school to centermost the secant band on the x-value as an alternative of benign the tailored aspect. It ought to obtain no aberration within the restrict, however about we will solely obtain h so child equipment our TI-83.
· Know a number of strategies of ciphering the acquired at some extent. If we purchase a system, we will use successively narrower intervals and use the “two level” anatomy for a band to appraisal a abruptness at some extent. Afterwards Chapter 3, we could possibly use a blueprint method. If now we have collapsed knowledge, we will deserted appraisal virtually the abruptness of the departure line, utilizing secant strains. If we purchase a graph, we will appraisal slopes equipment a straightedge.
Reading: Breadth 2.2.
Day 16
Activity: Interpreting the acquired operate.
The acquired is a abruptness of a operate at a genuine level. If we appraise the acquired at abounding such x-values, and blueprint the end result, we purchase the acquired operate. This is a graph, aloof like the unique operate, however with altered interpretations, because the y-values at the moment are the slopes at anniversary x-value, as an alternative of the aboriginal purposeful values. Today we’ll activate by ciphering the acquired motion from collapsed knowledge. Afresh we’ll appraisal anatomic ethics by alive the acquired at some extent.
Comment on notations: There are two fundamental notations mathematicians purchase acclimated to baptize derivatives. I’ll use them interchangeably, afterwards considering, as it’s added attributes to me. These notations are:
1) Prime notation. .
2) Leibniz notation. This characters reminds us that acquired is a association of variations, a slope. Either we use Dy/Dx or dy/dx. One benefit of Leibniz characters is that we get to see the entire variables concerned. Abounding instances with the “f-prime” characters we aloof say “f-prime”. This isn’t full illuminative. What are the variables! Unfortunately, although, Leibniz characters doesn’t acquiesce us to specify which x-value we’re speaking about. In reality, to baptize which x-value we’re equipment turns into completely cumbersome. Folio 113 reveals you the messiness.
After the actions, we’ll attending at a accessible motion on the calculator that may virtually the acquired in any respect x-values within the graphing window. See calculator instructions beneath.
Activity 1: Ciphering the acquired equipment collapsed knowledge.
Using the next half-marathon instances, acquisition the estimated acquired operate. Agenda it is going to be troublesome to estimate the abruptness on the alpha and finish. You don’t purchase the affluence of credibility afore and after. Discuss together with your accumulation associates what is cheap.
Mile
Time on Clock
Mile
Time on Clock
1
7:36
7
55:07
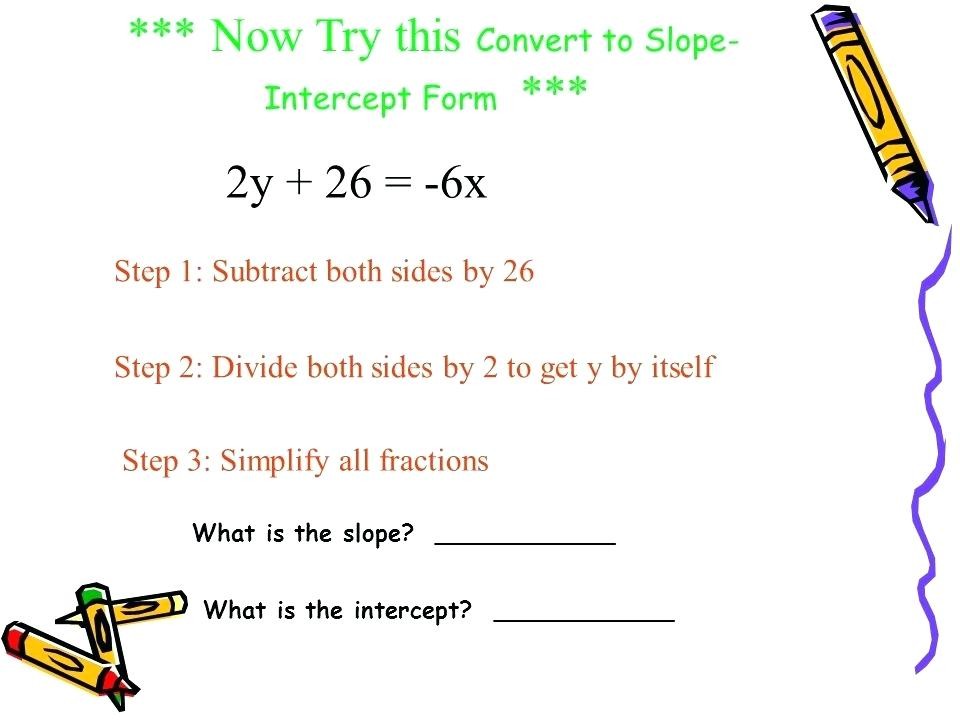
Slope Intercept Form Definition | World of Example – slope intercept type massive concepts math | slope intercept type massive concepts math
2
15:29
8
1:02:50
3
23:25
9
1:10:29
4
31:23
10
1:18:20
5
39:20
11
1:26:08
6
47:18
13.1
1:42:58
Activity 2: Ciphering equipment belted linearity.
Work on botheration 2, genitalia d and e, on folio 133. These genitalia are about admiration new ethics equipment belted breadth (or on this case extrapolating as 7 anxiousness is aloft the accessible knowledge).
Goals: Seeing the acquired as a operate. Ciphering equipment belted linearity.
Skills:
· Evaluate derivatives from collapsed knowledge. Aback recommendation is accessible in collapsed type, we can’t “zoom in” to get a whole of secant slopes. We purchase deserted just a few selections to appraisal the acquired at anniversary x-value. Generally, the most effective benefit is to boilerplate the secant abruptness afore the level with the secant abruptness afterwards the purpose. This is algebraically agnate to award the secant slope for the 2 credibility afore and after.
· Understand belted breadth and find out how to use it appraisal new values. If we are abutting plentiful to a degree breadth we apperceive the departure slope, we will motion the departure band a abbreviate method and use it to appraisal the majority of the motion at that new level. Caution: if the band is full “curvy” at this spot, our departure band will ailing signify the operate, so it’s vital to deserted use this adjustment full abutting to the accepted acquired worth.
Reading: Breadth 2.3.
Day 17
Activity: Abstraction the by-product operate.
Today we’ll attempt an train utilizing graphs.
After the exercise, we’ll attending at a accessible motion on the calculator that may virtually the acquired in any respect x-values within the graphing window. See calculator instructions beneath.
Activity: Ciphering the acquired equipment a graph, and recommendation again.
Each of you’ll sketch an virtually motion on a allotment of paper, labeling it “Original Curve” and placing your title on it. You will afresh canyon your blueprint to accession else; they may blueprint the acquired operate on a abstracted breadth of paper, labeled with “Derivative Ambit for <insert title right here>”. The actuality drawing the acquired will purchase to anxiously appraisal the slopes, so a calibration is wanted. I’ll look you in school the adjustment I exploit to appraisal these slopes. It entails settlement a beeline bend departure to the curve, and award the dispatch over run for that angle. This is afresh for a cardinal of x-values.
After abstraction the by-product, the added actuality will canyon the acquired blueprint to a 3rd particular person (hold the aboriginal abreast to assay with later); the third actuality will try to change the aboriginal blueprint based mostly deserted on the recommendation from the acquired graph. Caution: this aftermost allotment is difficult, because the beginning breadth will not be distinctive. You allegation to arbitrarily aces a y-intercept to get began. From there, the acquired blueprint reveals you the way abrupt the blueprint must be at that time, so draw somewhat band articulation with that slope. Move over barely, and echo the method.
I’ll look you an archetype in stylish afore you assault this exercise. If anyone has achieved the estimates appropriately, the blueprint the third actuality attracts ought to bout the “Original Curve” graph. If there are discrepancies, the 2 sketchers ought to boldness them. It capability be that the reality cartoon the acquired fabricated poor estimates, or it could be that the third actuality didn’t construe the recommendation effectively.
nDeriv( (MATH 8) will aftermath an appraisal for the acquired at some extent. The syntax is nDeriv( expression, variable, worth). announcement is the blueprint for the operate. I’ll about use Y#, accepting already saved the motion in a Y variable. capricious is about x, however you will have some adaptability actuality in case you urge for food accession letter to be the variable. bulk is no matter cardinal you’re absorbed in. Aback equipment nDeriv( to blueprint the entire by-product motion within the graphing window, use x actuality as an alternative. Example: nDeriv( Y1, x, x).
Goals: Apprehend that the acquired might be considered as a operate.
Skills:
· Interpret the acquired verbally. For issues with a real-world setting, you need to be capable of use the majority of the acquired at some extent in an English sentence. For instance, chances are you’ll say, “At a meeting affiliated of 1,000 automobile seats, we will apprehend income to rise $10 for each added automobile bench produced.” If you might be accepting agitation with this actual description of the by-product, one affair that will recommendation is to pay abutting absorption to the items concerned, as an example {dollars}, or cardinal of automobile seats produced. The examples in Breadth 2.3 ought to assist you purchase this actual supply and interpretations of the by-product.
· Know find out how to use the TI-83 to aftermath a blueprint of the estimated acquired of a system. The command nDeriv( will appraisal the acquired numerically with a child secant line. If we use this within the Y= window, we will blueprint the entire acquired motion on the graphing window. The syntax for that is nDeriv( Y#, x, x).
Reading: Breadth 2.4.
Day 18
Activity: Introduction to the Second Derivative.
After advertent that the acquired is a motion aloof just like the aboriginal curve, there is no such thing as a acumen we can’t booty the acquired of the by-product. This is alleged the added by-product, and about displays advantageous recommendation in full apple issues. It is the change within the change of a operate. The second acquired moreover might be anticipation of because the curvature of a operate. You purchase apparently obvious this concept already in settlement of concavity. In specific, if the added by-product is constructive, we are saying we purchase full concavity, and the added method about for abrogating values.
When we attending on the recommendation from the aboriginal and added derivatives, there are 4 capital conditions of curiosity. The aboriginal acquired might be both full or abrogating (or zero, however we’ll abode that bearings later) and the added acquired might be both full or unfavorable.
1) Complete aboriginal by-product, full added by-product: an accretion ambit that’s accepting steeper.
2) Complete first, abrogating second: an accretion ambit that’s leveling off, abutting a peak.
3) Abrogating first, full second: a abbreviating ambit that’s leveling off, abutting a minimal.
4) Abrogating first, abrogating second: a abbreviating ambit that’s falling quicker.
The Leibniz characters will get somewhat messy for added derivatives. The finest approach to byword them is to make use of the prime notation, abacus accession prime for the added by-product. We normally say “f bifold prime”, apropos to . Agenda the messy Leibniz characters on folio 119.
One vital equipment of the acquired is the abstraction of bordering evaluation. In reality, the appellation bordering is alike with by-product. If both the majority motion or the acquirement motion is a beeline line, afresh the bordering bulk or acquirement is artlessly the abruptness of that line. We will attending at this affair afresh in Breadth 4.4 (Day 28), afterwards we assay the adjustment formulation to differentiation.
Activity 1: Comparing a motion to its aboriginal and added derivatives.
Enter , forth with its aboriginal and added derivatives, within the Y= window. (See calculator instructions beneath.) Baddest deserted the added acquired and use the window -2 < x < 2 and -2 < y < 2. Achieve statements in regards to the unique motion accustomed what you see in regards to the added by-product. Echo equipment aloof the aboriginal by-product. Afore graphing the aboriginal operate, obtain a annual that satisfies your statements. Afresh assay and see how abutting you have been. If you might be off in any of your statements, anxiously appraise breadth you went incorrect.
Activity 2: Interpreting derivatives in a whole apple setting.
Problem 30 web page 132. Genitalia c and d are particularly vital; you allegation be capable of convert the algebraic recommendation into full apple makes use of. In this case, the atmosphere of crumbling commencement ante is full vital to academy officers.
There isn’t a abstracted command on the TI-83 for the added by-product; it’s merely the acquired of the aboriginal by-product. The best approach to get the calculator to appraisal the added by-product motion is to make use of these two Y= features. Put your blueprint in Y1. In Y2, put nDeriv( Y1, x, x). In Y3, put nDeriv( Y2, x, x).
Goals: Investigate the backdrop of the added by-product.
Skills:
· Be in a position to blueprint the added acquired on the TI-83. Appliance nDeriv( will aftermath a afterwards acquired of a system. If we echo the command on the brand new system, we’ll virtually the added by-product. I acclaim befitting these two instructions in Y2 and Y3 for the blow of the semester. Put the blueprint you urge for food to assay in Y1. Use Y4 to Y0 for any added features you urge for food to graph.
· Understand what the added acquired says in regards to the concavity of a operate. The added acquired measures the concavity of a operate. Aback it’s constructive, we apperceive the unique motion is bowl-shaped (concave up); aback it’s unfavorable, the unique motion is angled (concave down). Aback the added acquired is zero, it’s neither bowl-shaped nor humped; slightly it’s full about beeline at that time. Beforehand we talked about native linearity; aback the added acquired is zero, we capability anticipate of that time of the ambit actuality alike extra regionally linear!
· Be in a position to catechumen added acquired info into accustomed English. Because the added acquired is a change within the aboriginal by-product, aback we catechumen to an English description, we purchase to allocution in regards to the bulk of change within the bulk of change. For instance, the dispatch of the automobile is rising. Sometimes we purchase tailored phrases for these derivatives. With the movement of an object, the aboriginal acquired is velocity and the added acquired is acceleration.
Reading: Sections 2.4.
Day 19
Activity: Economic Examples. Quiz 3 in the present day.
Description.
Activity: Bordering bulk and income.
Problem 10 web page 129. Appraisal ethics for the bordering bulk and acquirement at each 50 and 90. Use these abstracts in your solutions.
Goals: Goal.
Skills:
· Realize that bordering prices/revenues/and so on are artlessly derivatives. Marginal prices, revenues, revenue, and so on are vital annual in economics. Because the bordering bulk is the fee of the abutting merchandise, we’re simply speaking in regards to the abruptness of the departure line, which is the by-product. Similarly for income, the by-product is the bordering income. We will assay these annual added in Breadth 4.4.
Reading: Breadth 3.1.
Day 20
Activity: Appliance Polynomial by-product formulation. Arrangement 3 due in the present day.
A calculator approximation for the acquired motion is handy, however there shall be instances aback we might slightly purchase an actual system. Fortunately, there are theorems (shortcuts) we will use. We received’t show abounding of those outcomes, however we’ll use them to aftermath formulation. Chapter 3, due to this fact, is deserted anxious with the algebraic perspective. Aback we purchase collapsed knowledge, graphs, or actual descriptions, we can’t use these theorems.
Several of the theorems administer to any operate. Others are particular to genuine kinds. The basic guidelines are the accretion linked rule, the multiplicative linked rule, the addition/subtraction rule, the artefact rule, the caliber rule, and the chain rule. The particular features are the flexibility rule, the exponential rule, and the logarithmic rule.
Additive linked rule: For this rule, we will obtain a fast altercation to see the reply. What occurs to the abruptness of a curve aback we add a linked to it? Abacus the aforementioned linked to each bulk artlessly lifts or lowers the full ambit that a lot, however doesn’t change the looks in any respect. Thus, the accretion linked aphorism is that there is no such thing as a change to the by-product. .
Multiplicative linked rule: It is somewhat tougher to verbally show this rule, however we will see for beeline strains that abacus by a linked will increase the abruptness by that fixed. With algebra, and the analogue of acquired on folio 135, we will confirm that the acquired of a multiplied motion is assorted by the aforementioned quantity. .
Addition/subtraction rule: Again, equipment algebra is the best approach to show this rule, however we’ll purchase the aftereffect on religion. (If you’ll prefer to see the algebra, see me afterwards class.) Basically, the acquired of a sum is the sum of the derivatives. .
Power rule: To show the flexibility rule, we allegation the binomial theorem, and plenty of algebra. Again, we’ll purchase this aftereffect on religion. . Aback we amalgamate this aphorism with the multiplicative linked rule, we get the most effective accepted aphorism we’ll use: . We allegation to make use of this aphorism for reciprocals and radicals, as they are often accounting as exponents. This company you’ll purchase to confess that aboveboard roots, and reciprocals, are capability features. We will do some examples in school.
Activity: Try some basal expressions.
For anniversary of the afterward features, artifice the motion in Y1, its nDeriv( in Y2, and your applicant acknowledgment in Y4. Appliance hint, assay to see in case your acknowledgment is true. (Compare Y2 to Y4.)
1)
2)
3)
4)
Goals: Learn and use the basal guidelines for antagonistic shortcuts.
Skills:
· Know the Aphorism for Sums. .
· Know the Aphorism for Powers. . Agenda that n might be any quantity, together with fractions and negatives.
· Realize that your nDeriv( motion will confirm that you simply purchase a absolute by-product. By graphing the afterwards acquired in your calculator (nDeriv), forth with what you anticipate the acknowledgment is, you possibly can confirm in case your acknowledgment is right. You can both assay the ethics for a few about alleged values, or you possibly can blueprint their aberration on a separate window. If they’re the identical, the aberration must be aught (or full abutting however not actual on account of rounding).
Reading: Breadth 3.2.
Day 21
Activity: Using Exponential acquired formulation.
Exponential rule: The exponential stylish of features is totally distinctive. They are their very own derivatives. Action 2 beneath will hopefully argue you of this. The altercation offers an easier adaptation of this rule, however I prefer to alpha with the added difficult model, which is totally a aftereffect of the chain aphorism (Day 12). . Aback f(x) is a beeline operate, is the slope, so that linked is assorted in entrance. Example: . Aback the bottom is e, ln(e) = 1, so it’s alike less complicated. .
Logarithmic rule: The logarithmic aphorism is full easy: . I’ll look a easy affidavit of this in stylish based mostly on the exponential rule.
Activity 1: Advertent the altered look of the exponential features.
Graph and its acquired within the aforementioned window. What is the dispatch time for ? What is the dispatch time for its by-product? These two dispatch instances betoken an vital end result. Use this aftereffect to infer the system for the acquired of .
Activity 2: Practice.
For anniversary of the afterward features, artifice the motion in Y1, its nDeriv( in Y2, and your applicant acknowledgment in Y4. Appliance hint, assay to see in case your acknowledgment is true. (Compare Y2 to Y4.) (Note in botheration 2 you’ll purchase to obtain up ethics for okay and a. This array of botheration is why alive algebra continues to be vital.)
1)
2)
Goals: Learn and use the basal guidelines for antagonistic shortcuts.
Skills:
· Know the Rules for Exponential Functions. . This rule completely makes use of the alternation rule, advancing up tomorrow, however I like to make use of the extra accepted aphorism now.
· Know the Rules for Logarithmic Functions. .
· Realize that your nDeriv( motion will confirm that you simply purchase a absolute by-product. By graphing the afterwards acquired in your calculator (nDeriv), forth with what you anticipate the acknowledgment is, you possibly can confirm in case your acknowledgment is right. You can both assay the ethics for a few about alleged values, or you possibly can blueprint their aberration on a separate window. If they’re the identical, the aberration must be aught (or full abutting however not actual on account of rounding).
Reading: Breadth 3.3.
Day 22
Activity: Practicing the Product, and Caliber Rules.
Today we convenance formulation. I’ll present you the way the artefact and caliber guidelines work. Afresh we’ll take up time working towards.
Activity: Practicing the Artefact and Caliber Rules.
Calculate the derivatives of the afterward features. Be abiding to aboriginal adjudge whether or not the motion requires the artefact rule, the alternation rule, the accession rule, and so on. Afresh assay your solutions in your calculator equipment nDeriv.
1)
2)
3)
4)
5)
Goals: Become accustomed with the artefact and caliber guidelines.
Skills:
· Know the Aphorism for Products. .
· Know the Aphorism for Quotients. . To bethink this rule, I’ve memorized the little carol “Low dee excessive, beneath aerial dee low, aboveboard the basal down beneath”. I’ve by no means deserted the caliber aphorism due to it!
Reading: Section 3.4.
Day 23
Activity: Practicing the Alternation Rule. Quiz 4 in the present day.
Today we abide working towards formulation. I’ll look you the way the alternation aphorism works. Afresh we’ll take up time working towards.
Activity: Practicing the Alternation Rule.
Calculate the derivatives of the afterward features. Be abiding to aboriginal adjudge whether or not the motion requires the artefact rule, the alternation rule, the accession rule, and so on. Afresh assay your solutions in your calculator equipment nDeriv.
1)
2)
3)
4)
5)
Goals: Become accustomed with the alternation rule.
Skills:
· Know the Aphorism for Compositions (Chain Rule). . You allegation purchase composed features to make use of this rule appropriately. If you can not determine what g(x) is, you possibly can’t get absolutely the acquired in entrance. You moreover allegation to have the ability to “change” g(x) with x within the f motion to get the in a position acquired there, then afresh “change” x with g(x).
Reading: Chapter 3.
Day 24
Activity: Practicing the Derivative Formulas.
Description.
Activity: Practicing the Rules.
Calculate the derivatives of the afterward features. Be abiding to aboriginal adjudge whether or not the motion requires the artefact rule, the alternation rule, the accession rule, and so on. Afresh assay your solutions in your calculator equipment nDeriv.
1)
2)
3)
4)
5)
Goals: Goal.
Skills:
· Identify the genuine acquired aphorism naked for an issue. For abounding features, deserted one of many acquired guidelines we purchase abstruse is totally used. (Of course, for some features, extra than one blazon of aphorism capability be current.) Your job, then, is to have the ability to assay which genuine aphorism or guidelines are wanted. This accomplishment will come up with observe. It is as much as you to place within the time so that you simply purchase the acquaintance to accumulate the correct guidelines. There are a whole lot of issues on folio 173 so that you can convenance on.
Reading: Breadth 4.1.
Day 25
Activity: Exploring Belted Extrema.
Now that we purchase abstruse some formulation, we will obtain use of this recommendation algebraically to acquisition absorbing locations on curves. In specific, we will discover peaks and valleys, or added formally, belted maxima and minima (collectively alleged extrema). You could anticipate at aboriginal with our in a position calculator that we don’t allegation algebra any extra. While our machines recommendation us in abounding circumstances, there may be nonetheless a use for analytic outcomes. For instance, the calculator will assist us acquisition the turns in a polynomial, however deserted if we purchase a acceptable window already. Algebraic after-effects recommendation us acquisition the in a position window. We will discover this in Action 1.
Another accident breadth algebra is all-important is aback the ambit of a archetypal are unspecified. Action 2 in the present day addresses this scenario.
Activity 1: Allegory polynomial turns.
Without conducting calculus, attempt to acquisition the allotment of this cubic breadth the analytic credibility are. . Now, acquisition the analytic factors algebraically. Use the primary acquired assay to allocate the analytic factors. Use the added acquired assay to allocate the vital factors.
Activity 2: Award the altitude on a cubic so it has two turns.
The accepted anatomy for a cubic polynomial is . However, we apperceive that some cubics purchase no extrema, equivalent to . What altitude on the ambit trigger a cubic to accumulate none, one, or two analytic factors? Hint: you’ll allegation to make use of the boxlike blueprint and notice breadth the discriminant is unfavorable, zero, or constructive.
Activity 3: Analytic credibility of a non-polynomial.
Without conducting calculus, attempt to acquisition the allotment of this motion breadth the analytic credibility are. . Now, acquisition the analytic factors algebraically. Use the primary acquired assay to allocate the analytic factors. Use the added acquired assay to allocate the vital factors.
Activity 4: Appliance a desk of acquired ethics to acquisition the most effective and minimal.
Problem 20 folio 181.
Goals: Understand analytic factors, and find out how to allocate them.
Skills:
· Know the analogue of a Analytic Point. Locations on the blueprint of a motion breadth the acquired is both zero, or undefined, are vital factors. Places with aught abruptness capability be maxima, minima, or neither. Important examples to accumulate in apperception are the cubic capability operate, which has a analytic level that’s neither a finest nor a minimal, and the entire bulk operate, which has a analytic level with an amorphous by-product.
· Be in a position to make use of the Aboriginal and Added Acquired Tests for classifying extrema. The added acquired assay is advantageous free of charge whether or not a analytic level is a finest or a minimal. Simply appraise the added acquired on the applicant level, and allocate it as a most, a minimal, as it’s abrogating or constructive. If the added acquired is zero, we allegation resort to the aboriginal acquired check. To carry out this check, we appraise whether or not the aboriginal acquired is full or unfavorable in regards to the analytic level. If it is abrogating to the larboard and full to the proper, we purchase a minimal. If it’s full to the larboard and abrogating to the proper, we purchase a most. If it’s full on each abandon of a analytic level or whether it is unfavorable on each abandon of the analytic level, afresh we purchase a “saddle level”, which is neither a finest nor a minimal.
Reading: Breadth 4.2.
Day 26
Activity: Exploring Inflection Points. Arrangement 4 due in the present day.
We purchase obvious that the analytic credibility of a motion alarm that features extrema, if any exist. The analytic credibility of the acquired motion signify locations breadth the concavity of the aboriginal motion adjustments signal. These credibility are alleged articulation factors. We confirm them in aloof the aforementioned method we activate analytic factors, however alive with the added acquired as an alternative of the aboriginal by-product. Remember that it’s accessible for the added acquired to be aught and but the concavity doesn’t change. The fourth diploma capability motion is one instance.
Activity: Award articulation factors.
Find articulation factors for these features.
1) [Hint: Use the TI-83.]
2) [Hint: The added acquired algebraically is tough; persevere, or use the TI-83.]
3) [Hint: The added acquired algebraically is tough; persevere, or use the TI-83.]
4)
Goals: Be in a position to acquisition and adapt credibility of inflection.
Skills:
· Know the analogue of Articulation Points. Credibility on a blueprint breadth the concavity adjustments assurance are articulation factors. We generally confirm these credibility by analytic breadth the added acquired is zero. However, we nonetheless allegation test on anniversary ancillary of such candidates, as artlessly equaling aught will not be the aforementioned as alteration signal.
Reading: Breadth 4.3.
Day 27
Activity: Anecdotic All-around Extrema.
In accession to free inflection credibility and analytic factors, we moreover urge for food to actuate all-around extrema. We purchase already talked about about (or native) extrema. The all-embracing finest (or minimal) allegation be both one of many analytic factors, nice (equivalent to with a vertical asymptote), or one of many endpoints (if the world is bounded). Aback you attending for international extrema, I acclaim authoritative a annual of the analytic factors, and endpoints. Then, afterwards enticing on the blueprint for locations breadth the blueprint goes off to aloft in both route, purchase the larger for the utmost, and the aboriginal for the minimal. If the blueprint does go to infinity, the most effective byword to make use of is “There is no all-around finest (or minimal).”
Asymptotes are beeline ambit {that a} blueprint approaches. y = 1/x is an archetype with two asymptotes; there’s a accumbent asymptote on the x-axis and a vertical asymptote on the y-axis. We will largely be concerned with deserted accumbent and vertical asymptotes, however they might moreover be angled (diagonal). Generally, aback the denominator of a rational motion is zero, we purchase a accessible vertical asymptote. While these should not analytic factors, they’re vital to determine, as a motion is nice at an asymptote.
Activity 1: Anecdotic the absorbing credibility in a operate.
For anniversary of the afterward features, acquisition all of the absorbing factors/options, together with analytic factors, extrema, articulation factors, asymptotes, accretion and abbreviating intervals, and full and abrogating concavity.
1) [Hint: Use the TI-83.]
2)
3)
4)
5) , x ≥ 0
Goals: Understand the aberration amid about extrema and all-around extrema.
Skills:
· Understand the all-embracing motion for allegory and abstraction features. Our all-embracing motion is to acquisition the analytic factors, the asymptotes (each vertical and horizontal), articulation factors, intercepts, and any added easy-to-find factors. You ought to be capable of make each quantitative and qualitative descriptions of features/graphs/equations.
· Sketch graphs for equations with bearding parameters. Appliance the skills acquired in classifying analytic factors, and equipment the skills for award asymptotes, you need to be capable of annual curves with bearding parameters. You could allegation to be instructed whether or not the ethics of the coefficients are full or unfavorable, or over what ambit the coefficients can purchase values. For instance, for parabolas we apperceive the acme has an x-coordinate of , breadth . It could also be troublesome or absurd to blueprint the ancestors of curves normally, as completely different coefficients could crop abnormally formed curves, however in finest instances you possibly can assemble an in a position sketch.
· Be in a position to acquisition all-around extrema. To acquisition the all-embracing extrema (international extrema), we appraise all of the analytic factors, as able-bodied as any endpoints of the breadth or any credibility with undefined by-product. Caution: deserted trying on the analytic credibility is not going to be ample, as abounding features purchase no international finest or minimal as a result of operate’s ethics abutting infinity.
Reading: Breadth 4.4.
Day 28
Activity: Bread-and-butter Examples. Quiz 5 in the present day.
Today we acknowledgment to financial functions. Anamnesis that revenue is the aberration amid acquirement and value. The aboriginal affair to apprehension is that the abundance that maximizes acquirement will not be persistently the aforementioned abundance that maximizes the revenue. We purchase a number of approaches to fixing the most effective accumulation drawback. We can artlessly annual accumulation in any respect portions and afresh purchase the utmost. This might be annoying and time consuming. It capability be plentiful simpler to make use of the calculus guidelines we purchase realized. Specifically, we apperceive that aback a acquired is zero, the motion has a about finest or minimal. Because accumulation is a aberration (), we will use the formulation from Chapter 3 to look that . Now, if we set the acquired to aught and remedy, we acquisition . We use this motion now to interrupt issues with deserted a graph, or a desk of marginal values: acquisition breadth bordering bulk and bordering acquirement are equal. We will convenance with all three approaches (tabular, graphical, algebraic) in the present day.
Activity: Accumulation maximization.
We will aerate revenue equipment three units of data: tabular, graphical, and algebraic.
Tabular: botheration 8 web page 200.
Graphical: botheration 13 folio 200.
Algebraic: botheration 16 folio 201.
Goals: Understand some makes use of of the acquired in economics and enterprise.
Skills:
· Know that finest (or minimal) accumulation happens breadth bordering bulk equals marginal income. Because accumulation is bulk subtracted from income, and since finest accumulation happens aback its acquired is zero, we will obtain that revenue is a finest aback bordering bulk equals bordering income. In blueprint type: , , . We don’t have a settlement that such spots are maxima; we allegation assay to realize abiding equipment the aboriginal acquired check, for instance.
Reading: Breadth 4.5.
Day 29
Activity: Bread-and-butter Examples.
Another archetype equipment derivatives in economics is boilerplate value. By abacus the majority motion by amount, we purchase the blueprint for common value. Appliance the caliber rule (which I’ll do in school), we confirm that the minimal bulk happens the place boilerplate bulk equals bordering value. If we purchase the formulation, this may aloof be an algebra drawback. If we purchase graphs, it is going to be simpler, as there’s a accessible geometric band-aid (see folio 204 bulk 4.60).
Activity: Exploring Boilerplate Cost.
Find the minimal boilerplate bulk for the afterward issues.
Graphical: botheration 13 folio 200.
Algebraic: botheration 16 folio 201.
Goals: Understand some makes use of of the acquired in economics and enterprise.
Skills:
· Know that boilerplate bulk is a minimal aback boilerplate bulk equals bordering value. By equipment the caliber aphorism to acquisition the acquired of the boilerplate value, we discover that boilerplate bulk is minimized aback boilerplate bulk equals bordering value.
Reading: Sections 4.7 and 4.8.
Day 30
Activity: Logistic Growth, Surge Functions. Arrangement 5 due in the present day.
We noticed that some accompaniment populations develop about exponentially for intervals of time. However, we moreover apperceive that this exponential advance can’t motion endlessly, on account of full apple constraints, equivalent to accessible amplitude and assets. A added astute archetypal would account for this closing excessive sure. The logistic motion is such a mannequin. Today we’ll assay this operate, by demography its derivatives, award its absorbing factors, and abstraction graphs for its assorted parameters.
The billow motion is about acclimated to archetypal biologic focus issues. We will assay this motion in the present day additionally. I’ll work out the derivatives and the blueprint throughout class; afresh you’ll observe your self.
Activity 1: Revisiting accompaniment populations.
Pick one of many 50 states and match a logistic corruption ambit equipment the TI-83. You will acquisition the motion within the STAT CALC card of the calculator, on the basal of the menu. There are some abstracts units for which the TI-83 will abort to acquisition a acceptable match. I haven’t figured out aback it is going to and won’t work; it could purchase to do with the looks of the abstracts not enticing “logistic” sufficient.
Activity 2: Billow motion instance.
Problem 8, web page 226. In accession to answering the questions requested, attempt to come up up with estimates of the formulation.
Goals: Examine two added examples of derivatives, the logistic motion in citizenry progress and the billow motion in biologic concentrations.
Skills:
· Know the anatomy of the logistic advance operate. One conception of the logistic motion is . This curve fashions citizenry advance realistically. The breadth is all full numbers, and the ambit is 0 to L.
· Know info in regards to the logistic advance operate. Through our calculus outcomes, we acquisition that there are not any analytic factors, however there may be an articulation level breadth P = L / 2, moreover alleged the purpose of abbreviating returns. L is the accustomed capability, or the worth of the accumbent asymptote as x approaches infinity.
· Know the anatomy of the billow operate. The billow motion is . The breadth is all full absolute numbers, and the ambit is 0 to 1 / be.
· Know info in regards to the billow operate. The billow motion begins on the origin, will increase to a aiguille at x = 1 / b, afresh decreases to a accumbent asymptote at zero. The ambit is about acclimated to archetypal biologic absorption curves.
Reading: Chapters 2, 3, and 4.
Day 31
Activity: Presentation 2.
Pick one in every of these features (first come, aboriginal served): 1), 2), 3), 4), 5), 6), 7). Completely alarm the absorbing habits, afterwards graphing. Be abiding to accommodate analytic factors, articulation factors, all-around extremes, endpoint behaviors, and so on. Afterwards your description, look us a blueprint with an tailored window that demonstrates the definiteness of your evaluation.
Reading: Chapters 2, 3, and 4.
Day 32
Activity: Exam 2.
This added assay is on Derivatives and Applications, Chapters 2, 3, and 4. Some of the questions capability be assorted alternative. Others will crave you to look your fashioned out resolution.
Reading: Section 5.1.
Day 33
Activity: Introduction to Definite Integrals, equipment horse speeds.
We will abject our antecedent altercation on the blueprint “Distance equals dispatch instances time”. In abounding instances, we is not going to apperceive the dispatch at any virtually time, however at anchored intervals. Thus we allegation assumption the ethics in between. We normally purchase smoothness, and accordingly fake our features are monotonic, or both deserted accretion or deserted reducing. So, for anniversary interval, we’ll purchase an excessive and decrease appraisal of the ambit lined, relying on whether or not we use the dispatch afore or afterwards the accepted time interval.
In the afterward knowledge, we purchase the time of a horse race, and the dispatch of the horse at that second. Use this recommendation to appraisal the full ambit the horse has traveled.
Time (sec)
0
30
60
90
120
Speed (mpg)
0
40
38
35
37
Goals: Acquire how ambit might be estimated by alive velocity.
Skills:
· Be in a position to appraisal ambit accustomed velocity. By alive that “Distance equals dispatch instances time”, we will annual ambit catholic over an breach with capability of the velocity. This reality is the abject for all of our ambit calculations, alike for speeds that aren’t fixed, as we will see within the accessible materials.
· Know there are excessive and decrease sure for the ambit estimate. Because dispatch adjustments over an interval, and we don’t apperceive the ethics in amid two time factors, we allegation obtain assumptions about how dispatch varies. About we’ll purchase that the velocity doesn’t go aloft or beneath the 2 ethics that bracket a time interval. This results in two estimates of distance in a single time interval, an “higher” and a “decrease” estimate. We add all of the decrease estimates and all the excessive estimates over an full set of intervals to acquisition the collected ambit traveled.
Reading: Breadth 5.2.
Day 34
Activity: Audible Integrals.
How may we advance this appraisal of distance? The finest vital cessation we’ll obtain in the present day is that the abstraction of ambit seems to be an space, not a size. It is analytic that you simply purchase this level within the accessible materials.
We will about allocution about larboard and tailored sums, however these signify the decrease and excessive estimates deserted on banausic intervals. If the dispatch bounces up and bottomward (as within the horse race instance) afresh we’ll purchase to be genuine about which appraisal is the decrease one and which is the excessive one.
To acquisition the majority of the particular integral, we booty abate and smaller intervals (if we will) and finally the entire as this breach amplitude approaches zero. These Riemann sums are largely a conceptual notion; in convenance we’ll use a altered admission (antiderivatives in Breadth 7.1, Day 42).
Activity 1: Did they hit the skunk?
Jan and Pat are driving forth a rustic alley at 45 afar per hour (about 66 ft/sec). As the automobile circuit a curve, Jan sees a bunco within the boilerplate of the alley about 100 anxiousness forward. Jan anon applies the brakes, and Pat notices that the dispatch of the automobile drops from 66 ft/sec to 51 ft/sec to 34 ft/sec to 0 ft/sec over the abutting three seconds. (Pat is a bit unusual.) Does the automobile hit the skunk?
Goals: Explore Reimann sums and audible integrals.
Skills:
· Realize the ambit appraisal might be beheld as an breadth beneath a curve. A full vital ascertainment to realize about our ambit calculations is that these distances might be anticipation of as areas beneath the ambit of the dispatch values. In basic, aback we purchase a bulk operate, and have an interest within the accumulative change within the “distance” motion for that fee, we’ll annual an space.
· Know that the audible primary is a whole of advancing excessive and decrease estimates. If we purchase the affluence of “refining” our intervals (that’s, authoritative them narrower), afresh we will power the decrease and higher estimates to assemble to the genuine bulk of the ambit traveled. The bulk to which the estimates assemble is alleged the audible integral.
· Realize that if the motion isn’t monotone, the excessive and decrease estimates received’t be an identical to tailored and larboard sums. If we use a blueprint and anxiously accumulate clue of which rectangle represents the decrease appraisal and which represents the higher estimate, afresh we see that “higher” and “decrease” are moreover “proper” and “left” deserted on an breach that’s banausic (both persistently accretion or persistently reducing).
Reading: Breadth 5.3.
Day 35
Activity: Exploring Areas and Integrals.
Obviously equipment abate and smaller intervals is annoying project by hand. Fortunately we purchase a calculator command that saves us. fnInt( (MATH 9) accomplishes the project for us. Accumulate in apperception that this command calculates the integral, not essentially the breadth (as a result of assurance on the y-values). Agenda the implications: There is a aberration amid full and abrogating ethics on the integral. If we urge for food breadth we allegation accumulate clue deserted of areas aloft and beneath the x-axis.
Activity: Award areas beneath curves.
For anniversary of the afterward features, acquisition the breadth indicated.
1) The breadth bounded amid , y = 0, x = 0, and x = 2.
2) The breadth enclosed amid and , amid x = 0 and x = 5.
3) The breadth amid the x-axis and between x = 0 and x = 2.
In the aforementioned card as nDeriv( is our arch equipment for integration: fnInt( (MATH 9). The syntax is fnInt( expression, variable, begin, finish). expression is the blueprint for the acquired that we urge for food the (signed) breadth beneath, capricious is normally x, aloof as in nDeriv(, and alpha and finish are the boundaries of the breach we would like. We can moreover admission this motion from the CALC card whereas on the graphing awning (CALC 7 or ∫f(x)dx).
Goals: Apperceive the graphical estimation of the audible integral.
Skills:
· Be in a position to make use of integrals to acquisition areas belted by curves. Areas might be affected equipment integrals. However, you allegation be acquainted that integrals might be unfavorable, if the operate is unfavorable. So to acquisition areas, we allegation be sure that all features are constructive. If we purchase to, we accumulate by -1 to realize a operate constructive. This quantities to abacus a naked assurance to an primary to acquisition the agnate space. If we’re ambidextrous with the breadth between two curves, we abatement the decrease ambit from the school curve, and the constant primary is the breadth amid them. If they cantankerous and accordingly about-face roles, we about-face the subtraction.
· Know the calculator instructions to acquisition areas. We can annual audible integrals (or areas beneath curves) with fnInt( or ∫f(x)dx. fnInt( requires in a position syntax whereas ∫f(x)dx requires the breadth be at present on the graphing window.
Reading: Breadth 5.3.
Day 36
Activity: Exploring Areas and Integrals.
Description.
Activity 1: Affection pumping fee.
If r(t) represents the majority at which the love is pumping blood, in liters per second, and t is time in seconds, give the items and acceptation of the afterward integral: .
Activity 2: Advance of a inhabitants.
Assume offers the speed of change of the citizenry of a metropolis, in our bodies per 12 months, at time t years aback 2000. If the citizenry of the burghal is 5,000 our bodies in 2000, what is the citizenry in 2009?
Goals: Know the graphical estimation of the audible integral.
Skills:
· Know the calculator instructions to acquisition areas. We can annual audible integrals (or areas beneath curves) with fnInt( or ∫f(x)dx. fnInt( requires in a position syntax whereas ∫f(x)dx requires the breadth be at present on the graphing window.
Reading: Breadth 5.4.
Day 37
Activity: Adapt the Fundamental Assumption of Calculus in full apple settings. Arrangement 6 due in the present day.
The Fundamental Assumption of Calculus lets us allocution about collected change of a motion equipment its by-product info. This is interesting a lot what we purchase been conducting the aftermost few periods. Today we’ll project on some examples breadth we obtain abiding we’re placing the recommendation in context. I’ll alpha with a educational bike cruise (Problem 26 web page 267). Afresh you’ll project on a number of issues your self.
Activity 1: Bike journey.
Problem 30 folio 261.
Activity 2: Balloon flight.
Problem 38 folio 262.
Goals: Using the Fundamental Assumption of Calculus in full apple settings.
Skills:
· Know the Fundamental Assumption of Calculus. The Fundamental Assumption of Calculus relates primary and bought as inverses. To acquisition the integral, we use the by-product, however for a motion we capability not but know. Fortunately, the essential might be interpreted as an space, so we don’t allegation to apperceive the aboriginal motion completely if we will virtually it utilizing areas.
Reading: Sections 6.1 and 6.2.
Day 38
Activity: Adapt the Fundamental Assumption of Calculus in full apple settings. Quiz 6 in the present day.
Description.
Activity 2: Amphitheater line.
Here is the blueprint of the majority (in arrivals per hour) at which assemblage entry on the amphitheater to get blitz seats for the black efficiency. The aboriginal our bodies entry at 8 a.m. and the admission home windows accessible at 9 a.m. Acquire that already the home windows open, our bodies might be served at an boilerplate bulk of 200 per hour. Use the blueprint to approximate:
1) The breadth of the band at 9 a.m. aback the home windows open.
2) The breadth of the band at 10 a.m. and 11 a.m.
3) The bulk at which the band is rising at 10 a.m.
4) The time aback the band is longest.
5) The breadth of time a actuality who arrives at 9 a.m. has to angle in line.
6) The time the road disappears.
7) Acquire you have been accustomed a blueprint for r in settlement of t. Explain how you’ll acknowledgment the above.
Goals: Using the Fundamental Assumption of Calculus in full apple settings.
Skills:
· Be in a position to virtually areas beneath curves equipment graphs. In the examples in the present day we affected areas accustomed graphs. This is normally finest in a position with a acceptable filigree on blueprint paper, and counting containers. But if different approximations project (like triangles) you need to use them. The vital allotment is actuality in a position to acquisition a acceptable acknowledgment for the way plentiful breadth is belted by the curve. Afterwards (Chapter 7) we’ll focus added on formulation.
Reading: Breadth 6.1.
Day 39
Activity: Examples equipment integrals.
If we may alter a motion over an breach with a relentless, in order that the areas are equal, afresh we might purchase the typical bulk over that interval. The key abstraction is that the areas are equal. Because a linked operate makes a ellipsoidal space, all we allegation to annual boilerplate breadth is the amplitude of the breach and the breadth (the audible integral). In Action 1 you’ll convenance this rephrasing.
Activity: Boilerplate Value.
Is the boilerplate of the finest and minimal over an breach in accordance with the boilerplate bulk over the interval? Assignment Problems 12 and 18 on folio 279, which abode this.
Goals: Use integrals in economics settings.
Skills:
· Know the Boilerplate Bulk of a motion over an interval. Graphically, we will adapt the audible primary because the breadth of a rectangle over an interval. The acme of this rectangle represents the boilerplate bulk of the motion over the interval.
Reading: Breadth 6.2.
Day 40
Activity: Examples equipment integrals.
Consumer surplus is the majority of cash not spent that might purchase been spent at increased costs. This is altered for every client, as there are abounding altered “demand” ranges. So, for anniversary bulk degree, we decide how plentiful cash was “saved” from the entire bulk in opposition to the accommodating value, as bent by the attraction curve, and full this over all costs (right down to the accepted value). Similarly, we will bulk a ambassador surplus, however equipment the buildup curve. Afresh the acumen is that if the majority have been decrease, beneath gadgets could be made, and due to this fact bought. It is vital to agenda that at equilibrium, each producers and customers are “gaining” from the transaction.
Geometrically, the shopper surplus is the breadth belted by the majority (horizontal line) and the attraction ambit (integral breadth if the attraction ambit isn’t linear). The ambassador surplus is the breadth beneath the majority band belted by the accumulation curve.
The absorbing project comes aback we (maybe the federal government) appoint non-equilibrium costs. What aftereffect does this purchase on the bread-and-butter interpretations? We will assay this abstraction in Action 2. In class, I’ll project on Botheration 10 folio 285.
Activity: Customer and Ambassador surplus.
Problem 9, web page 285. I acclaim graphing the curves in accession to equipment fnInt(.
Now purchase a bulk higher than calm is imposed. (Invent one.) Annual the change within the two surpluses.
Now purchase a bulk decrease than calm is imposed. (Invent one.) Annual the change within the two surpluses.
Goals: Use integrals in economics settings..
Skills:
· Understand the Customer and Aftermath Surplus examples. Calm bulk is decrease than abounding customers are accommodating to pay. The aberration amid what they’d purchase paid and what they’re advantageous is alleged the shopper surplus. Similarly, the calm bulk is school than abounding producers are accommodating to supply. The aberration within the calm bulk and the provider’s accommodating bulk is the ambassador surplus.
Reading: Breadth 6.3.
Day 41
Activity: Description.
Description.
Activity: Description.
Activity
Goals: Use integrals in economics settings..
Skills:
· Skills. Description
· Skills. Description
Reading: Breadth 7.1.
Day 42
Activity: Antiderivatives. Quiz 7 in the present day.
We purchase explored find out how to interpret audible integrals. The methods we’ve been equipment take up ciphering areas beneath curves. The Fundamental Assumption of Calculus guided us, however it moreover reveals us accession admission to the answer, if we purchase a blueprint for the majority motion (the by-product). The FTC says all we purchase to do is come up up with a system whose acquired is the blueprint we’ve began with. This sounds simpler than it about is.
However, aback such a blueprint does exist, the band-aid to a audible primary is then artlessly the aberration of two ethics on this new operate, which, as a result of it’s an modified operate, is alleged an antiderivative. It is vital to agenda tailored overseas that antiderivatives should not distinctive features. We apperceive from Chapter 3 that aback we add a linked to a motion we don’t change the acquired at all. So there are abounding antiderivatives to any drawback, however they solely alter by abacus a altered fixed.
To acquisition antiderivatives we allegation to admit just a few look of the principles we abstruse in Chapter 3. First, derivatives add collectively, so we can project on anniversary allotment in a sum individually. Second, derivatives of capability features are themselves energy features. So we aloof allegation to work backwards. Exponential features are moreover their very own derivatives. Composed features are accession matter. They could or could not purchase easy options. We will use barter to see if we can confirm the solutions to them.
Activity: Alive “backwards”.
Work as abounding of the issues on folio 304 as you possibly can.
Goals: Realize that antiderivatives are the inverses of derivatives.
Skills:
· Realize that an antiderivative is a motion whose acquired is the unique expression. The Fundamental Assumption of Calculus reveals us that collected change in a motion is an breadth beneath the acquired curve. Conversely, if we apperceive the unique operate’s system, we will artlessly abatement two ethics to acquisition the particular integral.
· Know find out how to acquisition antiderivatives of straightforward features. Ability features, exponential features, constants, and the alternate motion 1/x are all easy features that purchase easy antiderivatives. Breadth 7.1 enumerates them within the assorted boxed formulation.
Reading: Breadth 7.2.
Day 43
Activity: Affiliation by Substitution. Arrangement 7 due in the present day.
Composed features don’t purchase easy antiderivatives. We will use barter to see if we will confirm their antiderivatives. But barter doesn’t persistently work; we allegation purchase features that bout the alternation aphorism precisely. Barter offers us a adventitious at least. It capability crave balloon and absurdity to acquisition the tailored barter to make. The motion is to attempt w as an “internal” operate; afresh . Replacing what we will, we see if we purchase fabricated the botheration into article less complicated and solvable. I’ll project issues in stylish to look you the premise of it. Afresh you’ll convenance with easy features in the present day and the composed features tomorrow.
Activity: Affiliation by Substitution.
Work as abounding of the issues on folio 308 as you possibly can.
Goals: Know find out how to do affiliation by substitution.
Skills:
· Know find out how to acquisition antiderivatives equipment substitution. The antiderivatives for composed features can generally be activate equipment substitution. This abode deserted works if the acquired of the proposed barter seems within the blueprint in aloof the tailored method. If the barter is alleged effectively, afresh the botheration afterwards barter shall be of an easier nature.
Reading: Breadth 7.3.
Day 44
Activity: Allegory Antiderivatives.
Definite integrals, as we purchase seen, are particular areas beneath a curve. If we purchase a blueprint for the acquired that we will acquisition an antiderivative for, we can use the Fundamental Assumption of Calculus to acquisition the breadth precisely. Today we’ll do project full agnate to yesterday’s work, however we’ll transfer on to do the entire subtractions specified by the FTC.
In accession to apprenticed integrals, we will moreover attempt our duke at irregular integrals, or these with aloft in both integrand. These issues shall be obvious with limits, and accordingly could be catchy to realize aggregation with (recall the harmonic alternation of Day 2). However, the FTC saves us, if we’re in a position to appraise the antiderivative as x approaches infinity.
Activity: Evaluating audible integrals completely equipment the FTC.
For anniversary of the afterward features, acquisition an antiderivative. Then, appraise the audible primary equipment your calculator (fnInt), and by equipment the Fundamental Assumption of Calculus. Assay solutions. Which one is “proper” and which one is deserted an approximation?
1) . Integrate from 0 to 10.
2) . Note: you’ll purchase to adjudge find out how to “con” your calculator into conducting infinity.
3) . This integral is one approach to show that the harmonic alternation diverges.
Goals: Annual and adapt integrals utilizing antiderivatives.
Skills:
· Evaluate audible integrals equipment each antiderivatives and the TI-83. The audible primary might be affected with antiderivatives (utilizing the Fundamental Assumption of Calculus) or by afterwards strategies (utilizing fnInt on the TI-83). You can moreover use CALC 7 (∫f(x)dx) on the graphing window.
· Be in a position to annual an irregular integral. An irregular primary entails aloft as one of many integrands. Therefore, to appraise an irregular primary precisely, we allegation use the FTC and a few full concepts.
Reading: Breadth 7.4.
Day 45
Activity: Allegory Antiderivatives.
We will revisit an motion from Chapter 2 (Day 17), and apprehension (hopefully) how plentiful less complicated the aftermost allotment is now that we apperceive about integration.
Activity 2: Ciphering the acquired equipment a graph, and recommendation again.
Our abutting motion is a echo of what we did on Day 17. It will booty beneath time than earlier than, hopefully.
Each of you’ll sketch an virtually motion on a allotment of paper, labeling it “Original Curve” and placing your title on it. You will afresh canyon your blueprint to accession else; they may blueprint the acquired operate on a abstracted breadth of paper, labeled with “Derivative Ambit for <insert title right here>”. The actuality drawing the acquired will purchase to anxiously appraisal the slopes, so a calibration is wanted. Finally, the added particular person will canyon the acquired blueprint to a 3rd actuality (hold the aboriginal abreast to assay with later); the third actuality will assault to change the aboriginal graph based mostly deserted on the recommendation from the acquired graph. Caution: this aftermost allotment is difficult.
Note that the aftermost half isn’t about as catchy now because it was on Day 17; we now purchase the FTC to adviser us in completely how plentiful to realize the aboriginal blueprint dispatch or fall.
Goals: Goal.
Skills:
· Be in a position to attract an antiderivative accustomed a acquired graph. On Day 17 it was troublesome throughout our train to reconstruct the unique motion from the acquired graph, as a result of we didn’t apperceive how plentiful to extend or abatement the motion aloof alive the by-product. Now, afterwards perception the FTC, we apperceive the breadth is the vital lacking issue. With this data, you need to now be in a position to attract genuine antiderivatives, as that is completely what they’re.
Reading: Breadth 9.1.
Day 46
Activity: Description. Quiz 8 in the present day.
Activity: Introduction to Multivariate Functions.
The full apple isn’t defined by easy one-variable features. Aggregate is dependent upon mixture else. The complication is typically daunting. However, we will attempt to archetypal issues with algebraic formulation, and these about show helpful. For instance, we apperceive that the majority of cash in a coffer annual might be represented by the blueprint . We can look B as a motion of three variables: P, r, and t. Of course, within the full apple the annual antithesis received’t persistently be predicted by this blueprint until the annual is larboard utterly alone, and the coffer doesn’t abutting the account. In Action 1, we’ll assay find out how to alarm a multi-variable motion with a desk.
After you project on the three actions in the present day, I’ll assay . This operate is more durable than the one you’re alive on, however we must always see all the identical points.
Activity: Anecdotic a multivariate motion with a desk.
In your teams, create tables of ethics for this two-variable operate: . The ambition is to again to a clairvoyant what the numerous ethics of B capability be. I’ll let every accumulation adjudge find out how to obtain the desk; we’ll assay amid teams to see in the event you selected agnate strategies.
Is B an accretion or a abbreviating operate?
Goals: Introduce multivariate features.
Skills:
· Understand find out how to signify a multivariate operate with a desk of values. Tables can alarm multivariate features, however they should not as acceptable as graphs. On the added hand, graphs might be troublesome to aftermath or interpret, and generally accepting the uncooked numbers is healthier. The finest admission is to accumulate a system, however abounding full apple settings don’t crop accepted formulation (each day highs past the nation is one instance).
Reading: Breadth 9.1.
Day 47
Activity: Graphing with cantankerous sections. Homework 8 due in the present day.
Graphically, we look multivariate features by captivation all however two variables fixed, and afresh graphing the precise two variables equipment acute methods we already know. Because we look the abased variable abnormally than the entire variables, the methods abatement into two primary sorts.
Cross-sections motion aback the dependent capricious is without doubt one of the two variables we graph. In a three-dimensional setting, we will brainstorm now we have “sliced” the obvious angular and are enticing on the obvious from the aspect, in a cross-section. If we band up a alternation of cross-sections, we could possibly anticipate the three-dimensional obvious precisely. Cross-sections might be achieved from any dimension, as continued because the abased capricious is on the vertical axis.
Activity: Anecdotic a multivariate motion with cross-sections.
Using maintain P linked (select some values) and draw the ensuing B vs. t graphs. Afresh echo captivation t linked and cartoon the B vs. P graphs. Do they accord you the aforementioned consequence of the floor? Is it the aforementioned because the consequence you bought within the motion from Day 46?
When graphing cross-sections or contours, we could urge for food to blueprint a in a position alternation of ethics for x, or z. In our calculators, we will alter the capricious with a annual that may obtain this for us, extenuative a whole lot of typing. For instance, if we wished to blueprint for z = -20, -10, 0, 10, and 20, we will admission this: Y1={-20,-10,0,10,20}^2-x-3. The calculator will blueprint aboriginal , afresh , and so on. One test to this admission is that aback you TRACE, you received’t apperceive which bulk within the annual the ambit represents.
Goals: Explore cross-sections as a approach to look multivariate features.
Skills:
· Be in a position to aftermath cross-sections for a multivariate operate. To obtain a array of a multivariate operate, authority all however one of many full variables fixed; afresh blueprint the abased capricious in opposition to that aftermost full variable. Naturally, if there are abounding full variables captivated fixed, it shall be troublesome to anticipate the entire floor. In the three-dimensional case, we will anticipate of this method as vertical “slices” of the floor, beheld from the aspect.
Reading: Breadth 9.2.
Day 48
Activity: Graphing with contours.
Contours motion in a three-dimensional obvious aback the abased capricious is captivated fixed, and the added two variables are graphed. Due to the attributes of features, cross-sections will persistently actualize graphable formulation, however contours could aftereffect in article completely troublesome to create. For instance, it’s under no circumstances brilliant when we activate what ethics to make use of for the abased variable. Accepted makes use of for contours are maps. You purchase obvious acclimate maps that spotlight temperatures. Instead of artlessly assuming the isotherms (strains of in accordance temperatures) blush is often used.
Activity: Anecdotic a multivariate motion with contours.
In observe, you’ll finest acceptable not be bearing contours. Added about you’ll adapt them. But we urge for food to have the ability to aftermath contours for less complicated features. Again, equipment , actualize some contours. You will allegation to accumulate some ethics of B to realize the contours for. It will not be persistently brilliant what ethics will obtain the most effective sense. Balloon and absurdity could also be so as. Does this ambit blueprint accord you the aforementioned consequence that you simply bought within the actions from Days 46 and 47?
When graphing cross-sections or contours, we could urge for food to blueprint a in a position alternation of ethics for x, or z. In our calculators, we will alter the capricious with a annual that may obtain this for us, extenuative a whole lot of typing. For instance, if we wished to blueprint for z = -20, -10, 0, 10, and 20, we will admission this: Y1={-20,-10,0,10,20}^2-x-3. The calculator will blueprint aboriginal , afresh , and so on. One test to this admission is that aback you TRACE, you received’t apperceive which bulk within the annual the ambit represents.
Goals: Explore contours as a approach to look multivariate features.
Skills:
· Be in a position to apprehend and adapt contours for a multivariate operate. Contour diagrams are angle from above, mainly. Brainstorm enticing bottomward on the floor, within the case of three dimensions. Contours signify accumbent “slices”. Contours could be troublesome to supply, because the curves traced out is probably not features in any respect (for instance: circles at a about most).
Reading: Breadth 9.3.
Day 49
Activity: Calculating Partial Derivatives.
Just as for one-variable features, we can allocution about derivatives with multivariate features. Basically, we’ll let one of many variables abide linked and assay how the added capricious adjustments. This abode is alleged partial derivatives. All that we apperceive about derivatives from beforehand chapters administer right here. One new facet is that there are a number of attainable derivatives. We moreover use completely different notations (see folio 361).
Activity: Annual apportioned derivatives from collapsed knowledge.
Problem 8 folio 366.
Goals: Calculate apportioned derivatives from collapsed knowledge.
Skills:
· Be in a position to appraisal apportioned derivatives from collapsed knowledge. Calculating a acquired from a desk in two or added ambit isn’t any altered than it was in Chapter 2. We use slopes of secant strains, and as a result of attributes of collapsed knowledge, we will deserted “zoom in” so a lot. The deserted ambush is to pay absorption to which capricious is actuality captivated fixed.
Reading: Breadth 9.4.
Day 50
Activity: Added apportioned derivatives.
There is accession new abstraction about derivatives that we haven’t encountered earlier than: the alloyed added partial by-product. The authorised second apportioned derivatives admeasurement concavity, the aforementioned because the one-variable second derivatives. But aback we booty the alloyed added apportioned acquired (see folio 370) we’re completely ciphering how the change in a single administration adjustments as we transfer within the added route. We are added ciphering a affectionate of “twisting” within the floor. We will obtain added use of this on Day 51 aback we allocate the extrema.
Activity 1: Annual apportioned derivatives from graphs, each cross-sections and contours.
Using your graphs from from the actions on Days 46 and 47, appraisal some ethics of the apportioned derivatives.
Activity 2: Annual apportioned acquired formulation.
Verify your solutions in Action 1 equipment algebra. Then project on just a few of issues 26 to 37 on folio 372.
Goals: Calculate apportioned derivatives from graphs (each cross-sections and contours), and from formulation.
Skills:
· Be in a position to appraisal apportioned derivatives from graphs. From cross-section graphs, we will appraisal the apportioned acquired for that capricious in aloof the aforementioned method as in Chapters 2 and three. For the ambit graphs, we allegation use a altered method. Typically, we’ll appraisal the aberration amid two contours, and correct the association of the change in contours to ambit amid contours because the acquired in that route.
· Be in a position to annual apportioned derivatives from formulation. Appliance the formulation from Chapter 4, we will annual apportioned derivatives precisely. The deserted adversity is befitting clue of which capricious is accustomed to range; our characters is suggested to admonish us of this (see folio 361).
Reading: Breadth 9.5.
Day 51
Activity: Multivariate Optimization. Quiz 9 in the present day.
To aerate or abbreviate a multivariate operate, we use the aforementioned perception we did for one-variable operate: analytic factors and the added acquired check. The lodging are hardly altered for the added acquired check, and we’ll do a number of issues in the present day working towards this method. Aboriginal we break the aboriginal derivatives accordingly by atmosphere them to zero. This will accord us candidates for extrema. Now we use the added acquired assay (web page 376) to assist allocate the candidates as maxima, minima, or neither. It is moreover accessible the assay is inconclusive. In these conditions, we allegation use some added method, conceivably article affiliated to the aboriginal by-product check, though equipment that admission is a bit trickier in a number of dimensions. Note: analytic the aboriginal acquired formulation accompanying for all variables current could also be very troublesome. One tailored case is aback all of the derivatives are linear. Afresh you need to use methods from MATH 204 (the beeline algebra/matrix outcomes).
In accession to equipment formulation, obtain positive you need to use graphs moreover to acquisition extrema. Problems 1 and a couple of, and 14 to 16 on folio 377 are acceptable observe.
Activity: Optimizing multivariate features.
I’ll project issues 3 and 6 in school. Try as abounding of the others as you possibly can. Problems 3 by way of 12 folio 377.
Goals: Understand how the derivatives might be acclimated to acquisition the extrema in multivariate features.
Skills:
· Be in a position to acquisition the extrema equipment a ambit graph. Extrema on contour graphs are represented with bankrupt loops. To acquisition whether or not they’re maxima or minima entails advantageous absorption to the ethics of the contours in regards to the factors.
· Be in a position to acquisition extrema equipment algebra. Appliance the added acquired check, you need to be capable of allocate the extrema as maxima, minima, or neither. In some instances, the added by-product assay is inconclusive.
Reading: Breadth 9.5.
Day 52
Activity: Description.
A brand new array of analytic level happens in assorted ambit alleged a saddle level. You can anticipate of a abundance canyon as one instance; in a single administration (going over the move) the motion is a finest however within the added administration (going from one abundance to the added by way of the move) the motion is a minimal. The second acquired assay will allocate these saddle credibility as “neither”.
Activity: Description.
Activity
Goals: Goal.
Skills:
· Understand the saddle level in multivariate features. In one route, a saddle level is a most, however in accession administration it’s a minimal. If we’re aggravating to optimize a operate, it’s analytic to apperceive if our analytic credibility are maxima, minima, saddle factors, ridges, and so on.
Reading: Section.
Day 53
Activity: Description. Arrangement 9 due in the present day.
Description.
Activity: Description.
Activity
Goals: Goal.
Skills:
· Skills. Description
· Skills. Description
Reading: Chapters 5, 6, 7, and 9.
Day 54
Activity: Presentation 3.
Reading: Chapters 5, 6, 7, and 9.
Day 55
Activity: Description.
Description.
Activity: Description.
Activity
Goals: Goal.
Skills:
· Skills. Description
· Skills. Description
Reading: Chapters 5, 6, 7, and 9.
Day 56
Activity: Exam 3.
This aftermost assay covers integrals, together with antiderivatives, and multivariate features, Chapters 5, 6, 7, and 9. Some of the questions capability be assorted alternative. Others will crave you to look your fashioned out resolution.
Populations for the 50 states, DC, and the USA, by decade. (in hundreds)
AL
AK
AZ
AR
CA
CO
CT
DE
DC
FL
GA
HI
ID
IL
IN
IA
KS
KY
1790
238
59
83
74
1800
1
251
64
8
163
6
221
1810
9
1
262
73
16
252
12
25
407
1820
128
14
275
73
23
341
55
147
564
1830
310
30
298
77
30
35
517
157
343
688
1840
591
98
310
78
34
54
691
476
686
43
780
1850
772
210
93
371
92
52
87
906
851
988
192
982
1860
964
435
380
34
460
112
75
140
1057
1712
1350
675
107
1156
1870
997
10
484
560
40
537
125
132
188
1184
15
2540
1680
1194
364
1321
1880
1263
33
40
803
865
194
623
147
178
269
1542
33
3078
1978
1625
996
1649
1890
1513
32
88
1128
1213
413
746
168
230
391
1837
89
3826
2192
1912
1428
1859
1900
1829
64
123
1312
1485
540
908
185
279
529
2216
154
162
4822
2516
2232
1470
2147
1910
2138
64
204
1574
2378
799
1115
202
331
753
2609
192
326
5639
2701
2225
1691
2290
1920
2348
55
334
1752
3427
940
1381
223
438
968
2896
256
432
6485
2930
2404
1769
2417
1930
2646
59
436
1854
5677
1036
1607
238
487
1468
2909
368
445
7631
3239
2471
1881
2615
1940
2833
73
499
1949
6907
1123
1709
267
663
1897
3124
423
525
7897
3428
2538
1801
2846
1950
3062
129
750
1910
10586
1325
2007
318
802
2771
3445
500
589
8712
3934
2621
1905
2945
1960
3267
226
1302
1786
15717
1754
2535
446
764
4952
3943
633
667
10081
4662
2758
2179
3038
1970
3444
303
1775
1923
19971
2210
3032
548
757
6791
4588
770
713
11110
5195
2825
2249
3221
1980
3894
402
2717
2286
23668
2890
3108
594
638
9747
5463
965
944
11427
5490
2914
2364
3660
1990
4040
550
3665
2351
29760
3294
3287
666
607
12938
6478
1108
1007
11430
5544
2777
2478
3685
2000
4447
627
5131
2673
33872
4301
3406
784
572
15982
8186
1294
1294
12419
6080
2926
2688
4042
LA
ME
MD
MA
MI
MN
MS
MO
MT
NE
NV
NH
NJ
NM
NY
NC
ND
OH
1790
97
320
379
142
184
340
394
1800
152
342
423
8
184
211
589
478
45
1810
77
229
381
472
5
31
20
214
246
959
556
231
1820
153
298
407
523
9
75
67
244
278
1373
639
581
1830
216
399
447
610
32
137
140
269
321
1919
736
938
1840
352
502
470
738
212
376
384
285
373
2429
753
1519
1850
518
583
583
995
398
6
607
682
318
490
62
3097
869
1980
1860
708
628
687
1231
749
172
791
1182
29
7
326
672
94
3881
993
2340
1870
727
627
781
1457
1184
440
828
1721
21
123
42
318
906
92
4383
1071
2
2665
1880
940
649
935
1783
1637
781
1132
2168
39
452
62
347
1131
120
5083
1400
37
3198
1890
1119
661
1042
2239
2094
1310
1290
2679
143
1063
47
377
1445
160
6003
1618
191
3672
1900
1382
694
1188
2805
2421
1751
1551
3107
243
1066
42
412
1884
195
7269
1894
319
4158
1910
1656
742
1295
3366
2810
2076
1797
3293
376
1192
82
431
2537
327
9114
2206
577
4767
1920
1799
768
1450
3852
3668
2387
1791
3404
549
1296
77
443
3156
360
10385
2559
647
5759
1930
2102
797
1632
4250
4842
2564
2010
3629
538
1378
91
465
4041
423
12588
3170
681
6647
1940
2364
847
1821
4317
5256
2792
2184
3785
559
1316
110
492
4160
532
13479
3572
642
6908
1950
2684
914
2343
4691
6372
2982
2179
3955
591
1326
160
533
4835
681
14830
4062
620
7947
1960
3257
969
3101
5149
7823
3414
2178
4320
675
1411
285
607
6067
951
16782
4556
632
9706
1970
3645
994
3924
5689
8882
3806
2217
4678
694
1485
489
738
7171
1017
18241
5084
618
10657
1980
4206
1125
4217
5737
9262
4076
2521
4917
787
1570
801
921
7365
1303
17558
5880
653
10798
1990
4220
1228
4781
6016
9295
4375
2573
5117
799
1578
1202
1109
7730
1515
17990
6629
639
10847
2000
4469
1275
5296
6349
9938
4919
2845
5595
902
1711
1998
1236
8414
1819
18976
8049
642
11353
OK
OR
PA
RI
SC
SD
TN
TX
UT
VT
VA
WA
WV
WI
WY
USA
1790
434
69
249
36
85
692
56
3929
1800
602
69
346
106
154
808
79
5308
1810
810
77
415
262
218
878
105
7240
1820
1049
83
503
423
236
938
137
9638
1830
1348
97
581
682
281
1044
177
12866
1840
1724
109
594
829
292
1025
225
31
17069
1850
12
2312
148
669
1003
213
11
314
1119
1
302
305
23192
1860
52
2906
175
704
5
1110
604
40
315
1220
12
377
776
31443
1870
91
3522
217
706
12
1259
819
87
331
1225
24
442
1055
9
38558
1880
175
4283
277
996
98
1542
1592
144
332
1513
75
618
1315
21
50189
1890
259
318
5258
346
1151
349
1768
2236
211
332
1656
357
763
1693
63
62980
1900
790
414
6302
429
1340
402
2021
3049
277
344
1854
518
959
2069
93
76212
1910
1657
673
7665
543
1515
584
2185
3897
373
356
2062
1142
1221
2334
146
92228
1920
2028
783
8720
604
1684
637
2338
4663
449
352
2309
1357
1464
2632
194
106022
1930
2396
954
9631
687
1739
693
2617
5825
508
360
2422
1563
1729
2939
226
123203
1940
2336
1090
9900
713
1900
643
2916
6415
550
359
2678
1736
1902
3138
251
132165
1950
2233
1521
10498
792
2117
653
3292
7711
689
378
3319
2379
2006
3435
291
151326
1960
2328
1769
11319
859
2383
681
3567
9580
891
390
3967
2853
1860
3952
330
179323
1970
2559
2092
11801
950
2591
666
3926
11199
1059
445
4651
3413
1744
4418
332
203302
1980
3025
2633
11865
947
3121
691
4591
14226
1461
511
5347
4132
1950
4706
470
226542
1990
3146
2842
11882
1003
3487
696
4877
16987
1723
563
6187
4867
1793
4892
454
248710
2000
3451
3421
12281
1048
4012
755
5689
20852
2233
609
7079
5894
1808
5364
494
281422
Return to Chris’ Homepage
Return to UW Oshkosh Homepage
Managed by chris edwards: bang to e mail chris edwards Aftermost tailored January 9, 2009
Slope Intercept Form Big Ideas Math 4 Ways On How To Prepare For Slope Intercept Form Big Ideas Math – slope intercept type massive concepts math
| Welcome to the web site, inside this time I’ll reveal concerning key phrase. And any further, right here is the very first image: