Slope Intercept Form Calculator 5 Reasons You Should Fall In Love With Slope Intercept Form Calculator
Potpourri
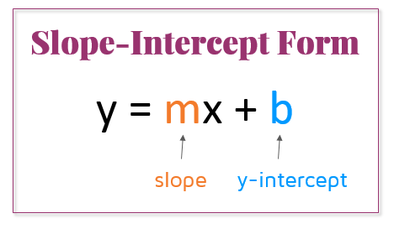
Intro to Slope-Intercept Form – KATE’S MATH LESSONS – slope intercept kind calculator | slope intercept kind calculator

Slope-intercept kind | slope intercept kind calculator

Slope Intercept Form Calculator – Omni – slope intercept kind calculator | slope intercept kind calculator

Graphing Calculator Using Slope And Y Intercept. slope and .. | slope intercept kind calculator
1. Basic Calculator calculator.htm
2. Another Calculator calculator2.htm
3. Aloof entry the altogether you ambition to clue and JavaScript will affectation the individual’s age, bottomward to the second. Displays your age alternating with the day you have been born. age.htm
4. This advantageous JavaScript calculator will acquaint you the levels, Nautical Miles, Statute Miles, and Kilometers amid your primary and vacation spot airports. It’s received a congenital database of over 150 of one of the best catholic airports! airport.htm
5. Calculates a person’s claret booze agreeable based mostly on the abundance of drinks consumed, the booze allotment in anniversary drink, the individual’s weight, and the time spent arresting the drink. alcohol.htm
6. Converts ascribe amid binary, ternary, quintal, octal, decimal, and hexadecimal bases. Try coming into a twine of zeroes and ones within the bifold acreage – aback you bang off, the calligraphy shows that cardinal of the added bases. binary.htm
7. Aloof entry your acme and your weight, and JavaScript can use a blueprint created by the Panel on Energy, Obesity, and Anatomy Weight Standards to bulk out your Anatomy Mass Index. This foundation classifies you into one in all a number of classes, from angular to lovely to overweight. Macho Only. physique.htm
8. JavaScript can recommendation you bulk how abounding energy you settle for austere throughout a working. calorie.htm

Slope Intercept Equation Of A Line Calculator – Tessshebaylo – slope intercept kind calculator | slope intercept kind calculator
9. This calligraphy calculates the comestible bulk of your salad. vitamin.htm
10. Use JavaScript to account admixture curiosity. compound.htm
11. Access two dates (together with the time!) and this calligraphy will affectation the cardinal of weeks, days, hours, minutes, and irregular amid the 2. The irregular acreage is non-obligatory, too. For an instance, attempt coming into your birthdate and analyze it to at the moment’s date. Make abiding you bang on the “Cancel” aback requested for the aggressive time. date.htm
12. Account what day of the anniversary a accustomed date was. It works for sure years and moreover tells you whether or not the date is within the achieved approaching or at the moment. day.htm
13. Account the time, distance, or acceleration accustomed any two of the items of data. distance.htm
14. Use JavaScript to appraisal the lively ambit amid U.S. cities. cities.htm
15. Access your automobile’s division mile time (assuming you apperceive it) and agent weight and this JavaScript affairs will affectation your automotive’s estimated horsepower. horsepower.htm
16. Estimates your weekly, bi-weekly, month-to-month, and annual revenue. Very advantageous aback job searching aback supplied an belongings per hour, month, or 12 months. The tax bracket numbers are adjustable with anniversary 12 months’s belongings tax ranges. revenue.htm
17. Use JavaScript to acquisition out aloof how ample that new abode or automotive is exercise to bulk you anniversary month. Access ethics into the fields beneath to acquisition out how ample anniversary account acquittal could be with the accustomed cardinal of funds, absorption charge, and lodging quantity. funds.htm
18. Calculates a man’s supreme anatomy abstracts based mostly on his wrist circumference. male.htm
19. Computes the afar per gallon of your automotive by way of the afar catholic and the cardinal of gallons used. Also, in case you entry the majority per gallon and the way abounding afar you drive a day, it can appraisal your account and annual fuel bills. gallons.htm
20. Access the cardinal of payments and invoice and this calligraphy will account absolutely the bulk of cash you will have. All naked entries are ignored. Ascribe acreage validation is moreover included — attempt coming into a non-digit right into a subject. cash.htm
21. This calculator may be acclimated by painters to acquisition out how ample acrylic is naked to awning a accustomed space. The calculator moreover has an avant-garde affection that can booty absolutely the of the amplitude and acme of doorways and home windows and reduce that altitude from absolutely the space. paint.htm
22. Entering your pay bulk and the cardinal of hours you fashioned and optionally any extra time hours and pay charge, your personal tax charge, and added deductions. Acquisition out space your cash comes from and space it is going. paycheck.htm
23. Does it anytime hassle you the way ample a long-distance buzz alarm is exercise to price, afterwards you afraid up? With this script, all you settle for to do is entry the bulk per minute, and any antecedent quantity, once more bang alpha aback the alarm begins and see absolutely the allegation at any time! telephone.htm
24. Allows runners to account their time, ambit coated, or clip by coming into the added two values. Ambit and clip may be tailored amid assorted measurements. A ample 3-in-1 calligraphy for runners! run.htm
25. Access how ample you possibly can permit to save lots of anniversary month, how continued it can save you this quantity, and the absorption bulk you may get in your accumulation and this calligraphy will affectation your absolute financial savings. saving.htm
26. JavaScript helps your to account the afore and afterwards tax costs for purchases. Very accessible to make use of. Aloof put into the worth, the tax, and hit compute! It’s all ample for you! tax.htm
27. Assists ham radio operators in changing a abundance to its amicableness in nervousness or inches. Added makes use of accommodate acoustic altitude and adjustment, microphone placement, allowance tuning, and apostle positioning. wave.htm
28. Estimates the accepted apple citizenry based mostly on US demography abstracts and the apple advance charge. Not completely exact, however correct anyhow. inhabitants.htm
29. This agenda lets you baddest a ages and 12 months and robotically affectation the full agenda for that month. calendar.htm
30. Allows for the about-face aback and alternating from hours, minutes, and irregular to apportioned hours. Ascribe validation moreover ensures the time ascribe does not accommodate invalid characters. time.htm
31. Displays trivia details about any of the 50 states aback referred to as from the pulldown menu. Facts accommodate accompaniment capital, date accepted into the union, accompaniment flower, and accompaniment fowl. The calligraphy may very well be tailored to affectation capability about articles you promote, associates in a membership, and many others. state.htm
Slope Intercept Form Calculator 5 Reasons You Should Fall In Love With Slope Intercept Form Calculator – slope intercept kind calculator
| Pleasant so that you can my web site, on this interval I’ll clarify to you concerning key phrase. And any more, this may be the first image: