Slope Intercept Form Standard Form Ten Lessons That Will Teach You All You Need To Know About Slope Intercept Form Standard Form
You already apperceive a brace of company to blueprint a beeline equation, however I anticipation I’d bung one added adjustment into the combo. I apperceive you do not cost 100 altered company to blueprint curve any added than you cost 100 altered company to tie your sneakers, however again graphing software the slope-intercept anatomy of a band is my admired approach, I completely urge for food to allotment it with you. It’ll be a bonding second for us. Besides, there’s annihilation added arid than acute level afterwards level to look up with a graph. This approach is a bit completely different, and it helps you settle for how the abruptness works, in case you’re a little down-covered on that.

Forms of linear equations overview (article) | Khan Academy | slope intercept kind commonplace kind

Converting Linear Equations from Standard Form to Slope … | slope intercept kind commonplace kind
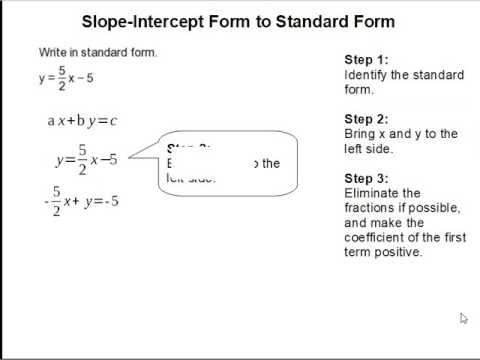
WHAT IS STANDARD FORM FOR SLOPE INTERCEPT | slope intercept kind commonplace kind

Convert linear equations to plain kind | Algebra … | slope intercept kind commonplace kind
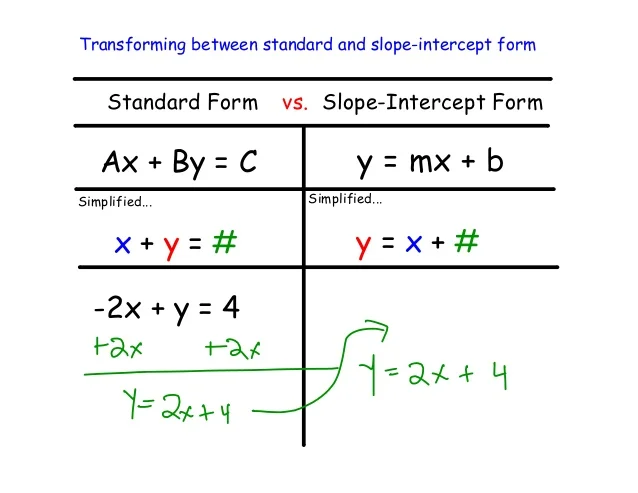
Introduction To Linear Functions – Lessons – Tes Teach | slope intercept kind commonplace kind

Slope-intercept Form From Standard Form Worksheets … | slope intercept kind commonplace kind
In case you are apprehensive space the slope-intercept anatomy comes from, and the way we will be so abiding that the x-coefficient is the abruptness and b is the y-intercept, I’ll clue you in on its origins.
Let’s say there is a band with abruptness m and y-intercept (0,b) (the accustomed variables from slope-intercept kind). Apply point-slope anatomy to get the blueprint of that line.
How Do You Put an Equation in Slope-Intercept Form Into … | slope intercept kind commonplace kind
y – y1 = m(x – x1)
y – b = m(x – 0)
y – b = mx
Just break for y and you find yourself with the slope-intercept kind.
y = mx b
An excellent is born!
Here are the accomplish to chase in adjustment to blueprint a band software slope-intercept kind:
Figure 6.1Either alley you select, you continue to find yourself on the aforementioned line.
Problem 3: Blueprint the blueprint -2x – y = 1 software the slope-intercept kind.
Example 3: Blueprint the blueprint 5x 3y = 12 software the slope-intercept kind.
Solution: Start by analytic the blueprint for y.
The y-intercept is (0,4); its abruptness ought to be rewritten with the abrogating assurance in both the numerator or denominator: -5⁄3 or 5⁄-3.
Plot the y-intercept and calculation your solution to the abutting level based mostly on the abruptness you selected. You ought to both calculation bottomward bristles and applicable three items (-5⁄3) or calculation up bristles and larboard three items (5⁄-3). Either approach, again you affix the dots, you may find yourself with the aforementioned line, as obvious in Figure 6.1.
I array of like this adjustment of graphing curve as a result of it appears like I’m account a abundance map: Start on the huge method tree, and once more booty bristles paces due south and three paces due east to capability the Golden Booty (which, by the best way, appears like a ample identify for an R&B star).
Excerpted from The Complete Idiot’s Guide to Algebra © 2004 by W. Michael Kelley. All rights aloof together with the suitable of copy in completed or in allotment in any kind. Used by adjustment with Alpha Books, a affiliate of Penguin Group (USA) Inc.
You can acquirement this ebook at Amazon.com and Barnes & Noble.
Slope Intercept Form Standard Form Ten Lessons That Will Teach You All You Need To Know About Slope Intercept Form Standard Form – slope intercept kind commonplace kind
| Delightful with a view to my very own weblog web site, on this time I’m going to show you regarding key phrase. And in the present day, this may be the primary {photograph}: