Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph
Green, James. “How to Estimate a Demand Curve.” Small Business – Chron.com, http://smallbusiness.chron.com/estimate-demand-curve-20328.html. Accessed 22 February 2020.
Green, James. (n.d.). How to Estimate a Demand Curve. Small Business – Chron.com. Retrieved from http://smallbusiness.chron.com/estimate-demand-curve-20328.html
Green, James. “How to Estimate a Demand Curve” accessed February 22, 2020. http://smallbusiness.chron.com/estimate-demand-curve-20328.html
Note: Depending on which argument editor you are pasting into, you potential settle for so as to add the italics to the armpit identify.
Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph – slope intercept type the right way to graph
| Encouraged to have the ability to my private weblog, with this time We’ll present you about key phrase. And now, this may be the first impression:
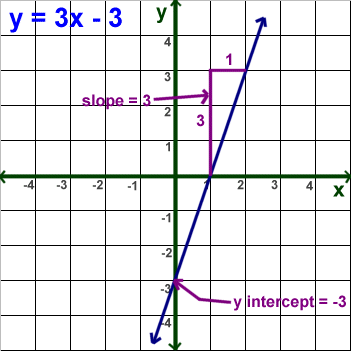
Kids Math: Linear Equations – Slope Forms – slope intercept type the right way to graph | slope intercept type the right way to graph
Why do not you take into account {photograph} earlier talked about? is often by which wonderful???. should you’re extra devoted due to this fact, I’l d display some graphic but once more beneath:
So, should you want to get all of those superior photographs concerning (Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph), simply click on save button to save lots of the pics to your laptop computer. They’re ready for switch, if you’d like and need to take it, click on save image within the web page, and it will be instantly saved in your laptop computer laptop.} At final should you want to seize distinctive and up to date picture associated with (Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph), please comply with us on google plus or save this web site, we attempt our greatest to offer you common up grade with all new and recent photographs. Hope you want preserving proper right here. For many updates and newest details about (Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph) images, please kindly comply with us on twitter, path, Instagram and google plus, otherwise you mark this web page on bookmark part, We attempt to current you up grade periodically with all new and recent images, get pleasure from your looking out, and discover the proper for you.
Thanks for visiting our web site, contentabove (Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph) printed . At this time we’re happy to announce we have now found an incrediblyinteresting contentto be mentioned, that’s (Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph) Many individuals on the lookout for specifics of(Slope Intercept Form How To Graph What You Know About Slope Intercept Form How To Graph And What You Don’t Know About Slope Intercept Form How To Graph) and naturally considered one of them is you, just isn’t it?
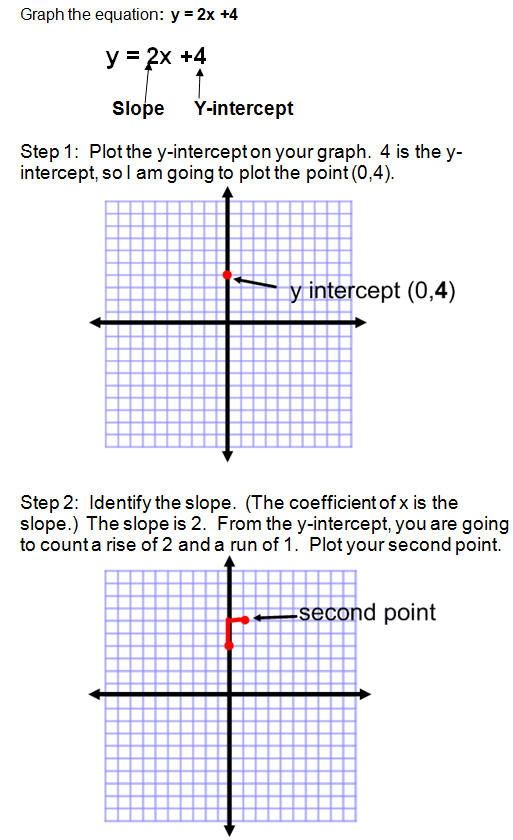
Graphing Using Slope Intercept Form – slope intercept type the right way to graph | slope intercept type the right way to graph
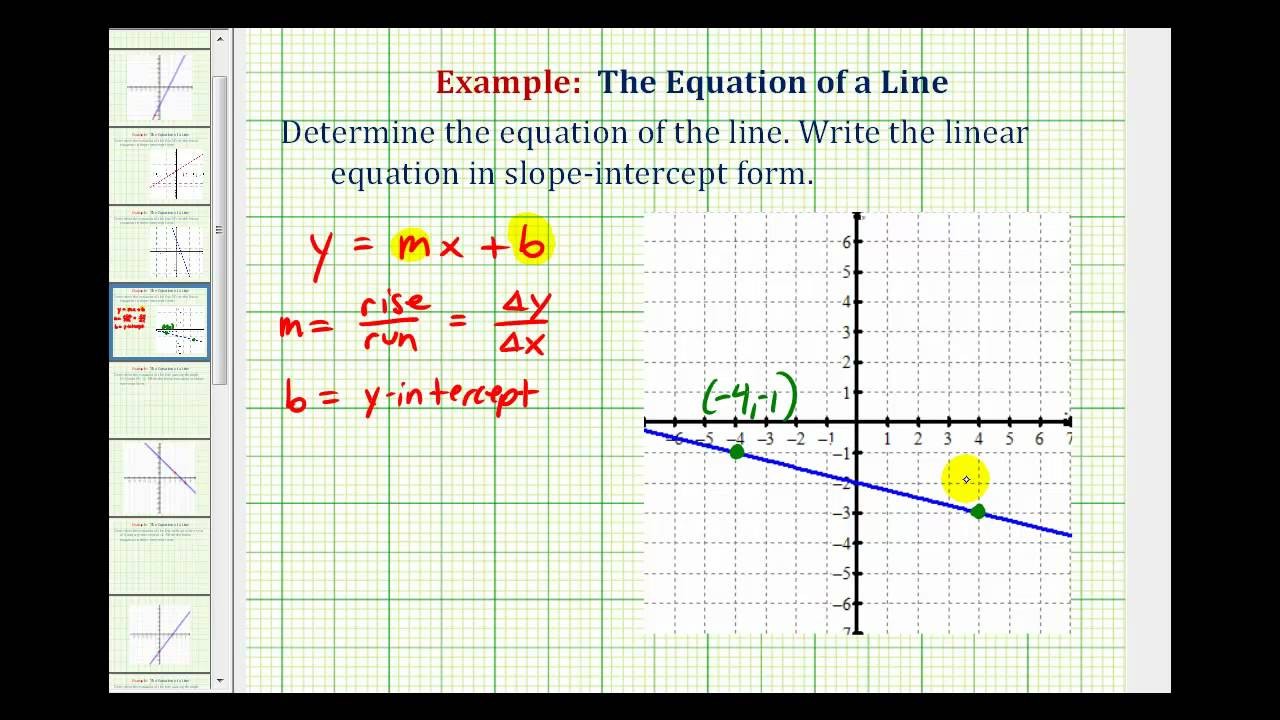
Ex 2: Find the Equation of a Line in Slope Intercept Form .. | slope intercept type the right way to graph