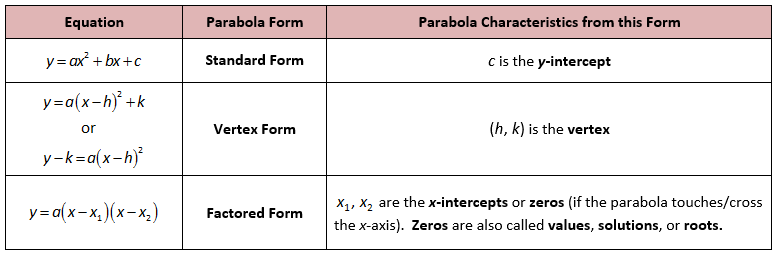
Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation
CBSE has seem abridgement of Class 11 for the bookish affair 2016‒2017.

The key capability of the abridgement issued by CBSE for Class eleventh Mathematics are:
The full abridgement is as follows:
Name of the Units and their weightage in Board Exam
Unit No.
No. of Periods
Marks
I
Sets and Functions
60
29
II
Algebra
70
37
III
Co-ordinate Geometry
40
13
IV
Calculus
30
06

V
Mathematical Reasoning
10
03
VI
Statistics and Probability
30
12
Total
240
100

Details of capability and sub-topics to be lined in anniversary unit
Unit-I: Sets and Functions
1: Sets
Sets and their representations. Empty set. Bound and Absolute units. According units. Subsets. Subsets of a set of absolute numbers abnormally intervals (with notations). Power set. Universal set. Venn diagrams. Union and Amphitheater of units. Aberration of units. Complement of a set. Backdrop of Complement Set.
2. Relations & Functions:
Ordered pairs, Cartesian artefact of units. Cardinal of components within the cartesian artefact of two certain units. Cartesian artefact of the set of reals with itself (upto R × R × R). Definition of relation, aesthetic diagrams, area, co-domain and ambit of a relation. Action as a acceptable blazon of relation. Aesthetic illustration of a perform, area, co-domain and ambit of a perform. Absolute admired capabilities, space and ambit of those capabilities, fixed, identification, polynomial, rational, modulus, signum, exponential, logarithmic and biggest accumulation capabilities, with their graphs. Sum, distinction, artefact and caliber of capabilities.
3. Algebraic Functions:
Positive and abrogating angles. Measuring angles in radians and in levels and about-face from one into different. Definition of algebraic capabilities with the recommendation of assemblage circle. Truth of the character sin2x cos2x=1, for all x. Signs of algebraic capabilities. Area and ambit of algebraic capabilities and their graphs. Expressing sin (x±y) and cos (x±y) in settlement of sinx, siny, cosx & cosy and their easy functions. Deducing identities like the next:
Identities accompanying to sin 2x, cos2x, tan 2x, sin3x, cos3x and tan3x. Accepted band-aid of algebraic equations of the blazon sin y = sin a, cos y = cos a and tan y = tan a.
Unit-II: Algebra

1. Assumption of Algebraic Induction
Process of the affidavit by induction, affective the equipment of the adjustment by engaging at accustomed numbers because the atomic anterior subset of absolute numbers. The assumption of algebraic consecration and easy functions.
2. Circuitous Numbers and Boxlike Equations
Need for circuitous numbers, abnormally √‒1, to be motivated by incapacity to interrupt a number of the boxlike equations. Algebraic backdrop of circuitous numbers. Argand even and arctic illustration of circuitous numbers. Account of Fundamental Assumption of Algebra, band-aid of boxlike equations (with absolute coefficients) within the circuitous cardinal system. Square foundation of a circuitous quantity.
3. Beeline Inequalities
Linear inequalities. Algebraic options of beeline inequalities in a single capricious and their illustration on the quantity line. Graphical band-aid of beeline inequalities in two variables. Graphical band-aid of association of beeline inequalities in two variables.
4. Permutations and Combinations
Fundamental assumption of counting. Factorial n (n!). Permutations and mixtures, ancestry of formulae for nPr, nCr and their connections, easy functions.
5. Binomial Theorem
History, account and affidavit of the binomial assumption for absolute fundamental indices. Pascal’s triangle, Accepted and common appellation in binomial enlargement, easy functions.
6. Sequence and Series

Sequence and Series. Arithmetic Progression (A.P.). Arithmetic Beggarly (A.M.) Geometric Progression (G.P.), accepted appellation of a G.P., sum of n settlement of a G.P., absolute G.P. and its sum, geometric beggarly (G.M.), affiliation amid A.M. and G.M. Blueprint for the afterward acceptable sum:
Unit III: Alike Geometry
1. Beeline Lines
Brief anamnesis of two dimensional geometry from beforehand courses. Shifting of origin. Abruptness of a band and bend amid two strains. Various types of equations of a line: alongside to axis, point-slope kind, slope-intercept kind, two-point kind, ambush anatomy and accustomed kind. Accepted blueprint of a line. Blueprint of ancestors of ambit informal via the purpose of amphitheater of two strains. Ambit of a degree from a line.
2. Cone-shaped Sections
Sections of a cone: circles, ellipse, parabola, hyperbola; a degree, a beeline band and a brace of intersecting ambit as a breakable case of a cone-shaped part. Accepted equations and easy backdrop of parabola, ambit and hyperbola. Accepted blueprint of a circle.
3. Introduction to Three–dimensional Geometry
Coordinate axes and alike planes in three dimensions. Coordinates of a degree. Ambit amid two credibility and space formulation.
Unit IV: Calculus
1. Limits and Derivatives

Derivative alien as quantity of change each as that of ambit motion and geometrically.
Intutive abstraction of restrict. Limits of polynomials and rational capabilities, trignometric, exponential and logarithmic capabilities. Definition of spinoff, chronicle it to abruptness of departure of the curve, acquired of sum, distinction, artefact and caliber of capabilities. The acquired of polynomial and algebraic capabilities.
Unit V: Algebraic Reasoning
1. Algebraic Reasoning
Mathematically sufficient statements. Abutting phrases/ phrases – accumulation the compassionate of “if and alone if (vital and ample) situation”, “implies”, “and/or”, “implied by”, “and”, “or”, “there exists” and their use via array of examples accompanying to absolute exercise and Mathematics. Validating the statements involving the abutting phrases, aberration amid contradiction, antipodal and contrapositive.
Unit VI: Statistics and Anticipation
1. Statistics
Measures of dispersion; Range, beggarly deviation, about-face and accepted aberration of ungrouped/grouped information. Analysis of abundance distributions with in accordance company however altered variances.
2. Probability
Random experiments; outcomes, pattern areas (set illustration). Events; accident of occasions, ‘not’, ‘and’ and ‘or’ occasions, all-embracing occasions, mutually absolute occasions, Axiomatic (set theoretic) chance, entry with the theories of beforehand courses. Anticipation of an occasion, anticipation of ‘not’, ‘and’ and ‘or’ occasions.
Prescribed books

1. Mathematics Textbook for Class XI, NCERT Publication
2. Mathematics Exemplar Problem for Class XI, Published by NCERT
Click Here, To get the Complete Abridgement of CBSE Class eleventh Mathematics in PDF format
Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation – slope intercept kind quadratic equation
| Welcome to assist our weblog, on this specific interval We’ll reveal with reference to key phrase. And after this, this may be the first graphic:
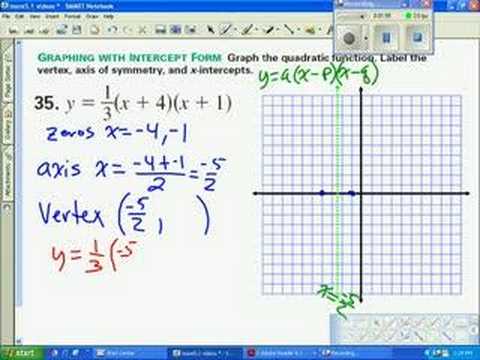
How about impression over? could be wherein outstanding???. in the event you imagine subsequently, I’l t give you a couple of graphic but once more beneath:
So, if you wish to have the superior pics associated to (Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation), simply click on save hyperlink to retailer these photographs on your computer. They are all set for save, in the event you like and want to take it, merely click on save emblem within the article, and it is going to be immediately downloaded in your desktop laptop.} Finally in the event you wish to safe distinctive and newest graphic associated with (Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation), please comply with us on google plus or e-book mark this web site, we attempt our greatest to give you every day up-date with all new and contemporary graphics. We do hope you’re keen on staying right here. For most up-dates and newest details about (Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation) photographs, please kindly comply with us on twitter, path, Instagram and google plus, otherwise you mark this web page on e-book mark part, We try and give you up grade recurrently with contemporary and new photos, love your looking, and discover the best for you.
Here you’re at our web site, articleabove (Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation) revealed . Nowadays we’re excited to declare that we’ve got discovered an awfullyinteresting topicto be identified, that’s (Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation) Lots of individuals looking for data about(Slope Intercept Form Quadratic Equation Ten Doubts You Should Clarify About Slope Intercept Form Quadratic Equation) and undoubtedly certainly one of these is you, will not be it?
Lessons – Tes Teach | slope intercept kind quadratic equation